题目内容
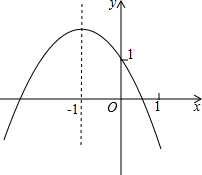 如图为二次函数y=ax2+bx+c(a≠0)的图象,下面四条信息:①4ac<b2<0;②4a+c<2b;③m(am+b)<a-b(m≠-1);④3a+c>0,其中正确信息的个数是( )
如图为二次函数y=ax2+bx+c(a≠0)的图象,下面四条信息:①4ac<b2<0;②4a+c<2b;③m(am+b)<a-b(m≠-1);④3a+c>0,其中正确信息的个数是( )| A、4个 | B、3个 | C、2个 | D、1个 |
考点:二次函数图象与系数的关系
专题:数形结合
分析:由抛物线与x轴有2个交点得到b2-4ac>0,即4ac<b2,而b2≥0,于是可对①进行判断;根据抛物线的对称性得到抛物线与x轴的另一个交点在(-3,0)和(-2,0)之间,则当x=-2时,y>0,即4a-2b+c>0,于是可对②进行判断;根据抛物线的最值问题,当x=-1时,y有最大值,即am2+bm+c<a-b+c(m≠-1),于是可对③进行判断;由抛物线的对称轴为直线x=-
=-1得到b=2a,再加上x=1时,y<0,即a+b+c<0,则可对④进行判断.
| b |
| 2a |
解答:解:∵抛物线与x轴有2个交点,
∴△=b2-4ac>0,即4ac<b2,
而b2≥0,所以①错误;
∵抛物线与x轴的一个交点在原点和(1,0)之间,
而抛物线的对称轴为直线x=-1,
∴抛物线与x轴的另一个交点在(-3,0)和(-2,0)之间,
∴当x=-2时,y>0,
∴4a-2b+c>0,即4a+c>2b,所以②错误;
∵抛物线的对称轴为直线x=-1,
∴当x=-1时,y有最大值,
∴am2+bm+c<a-b+c(m≠-1),即m(am+b)<a-b(m≠-1),所以③正确;
∵抛物线的对称轴为直线x=-
=-1,
∴b=2a,
而x=1时,y<0,即a+b+c<0,
∴a+2a+c<0,即3a+c<0,所以④错误.
故选D.
∴△=b2-4ac>0,即4ac<b2,
而b2≥0,所以①错误;
∵抛物线与x轴的一个交点在原点和(1,0)之间,
而抛物线的对称轴为直线x=-1,
∴抛物线与x轴的另一个交点在(-3,0)和(-2,0)之间,
∴当x=-2时,y>0,
∴4a-2b+c>0,即4a+c>2b,所以②错误;
∵抛物线的对称轴为直线x=-1,
∴当x=-1时,y有最大值,
∴am2+bm+c<a-b+c(m≠-1),即m(am+b)<a-b(m≠-1),所以③正确;
∵抛物线的对称轴为直线x=-
| b |
| 2a |
∴b=2a,
而x=1时,y<0,即a+b+c<0,
∴a+2a+c<0,即3a+c<0,所以④错误.
故选D.
点评:本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定,△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
2013年1-7月广州市财政收入增势稳定,完成地方公共财政预算收入653.6亿,将653.6亿元用科学记数法表示正确的是( )
| A、6.536×102亿元 |
| B、6.536×103亿元 |
| C、0.6536×103 |
| D、65.36×10亿元 |
 在1998年特大洪水时期,要加固全长为10000m的河堤.大堤高5m,坝顶宽4m,迎水坡和背水坡都是坡度为1:1的等腰梯形.现要将大堤加高1m,背水坡坡度改为1:1.5.已知坝顶宽不变,求大坝横截面面积增加了多少平方米?完成工程需多少立方米的土石?
在1998年特大洪水时期,要加固全长为10000m的河堤.大堤高5m,坝顶宽4m,迎水坡和背水坡都是坡度为1:1的等腰梯形.现要将大堤加高1m,背水坡坡度改为1:1.5.已知坝顶宽不变,求大坝横截面面积增加了多少平方米?完成工程需多少立方米的土石? 如图,已知△ABC.
如图,已知△ABC.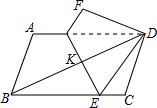 如图,已知四边形ABCD中,AB∥CD,AB=
如图,已知四边形ABCD中,AB∥CD,AB=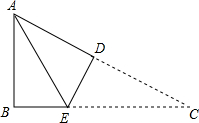 如图,在△ABC中,∠B=90°,∠C=30°,AB=3,BC=3
如图,在△ABC中,∠B=90°,∠C=30°,AB=3,BC=3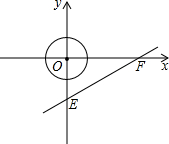 如图所示,在平面直角坐标系中,已知点E和F的坐标分别为E(0,-2)、F(2
如图所示,在平面直角坐标系中,已知点E和F的坐标分别为E(0,-2)、F(2 如图,直线y=x-3分别与x轴、y轴交于点P,F,与双曲线y=
如图,直线y=x-3分别与x轴、y轴交于点P,F,与双曲线y=