题目内容
6.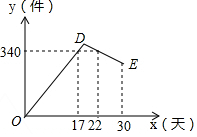 某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.
某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.(1)第24天的日销售量是330件,日销售利润是660元.
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)日销售利润不低于640元的天数共有多少天?试销售期间,日销售最大利润是多少元?
分析 (1)根据第22天销售了340件,结合时间每增加1天日销售量减少5件,即可求出第24天的日销售量,再根据日销售利润=单件利润×日销售量即可求出日销售利润;
(2)根据点D的坐标利用待定系数法即可求出线段OD的函数关系式,根据第22天销售了340件,结合时间每增加1天日销售量减少5件,即可求出线段DE的函数关系式,联立两函数关系式求出交点D的坐标,此题得解;
(3)分0≤x≤18和18<x≤30,找出关于x的一元一次不等式,解之即可得出x的取值范围,有起始和结束时间即可求出日销售利润不低于640元的天数,再根据点D的坐标结合日销售利润=单件利润×日销售数,即可求出日销售最大利润.
解答 解:(1)340-(24-22)×5=330(件),
330×(8-6)=660(元).
故答案为:330;660.
(2)设线段OD所表示的y与x之间的函数关系式为y=kx,
将(17,340)代入y=kx中,
340=17k,解得:k=20,
∴线段OD所表示的y与x之间的函数关系式为y=20x.
根据题意得:线段DE所表示的y与x之间的函数关系式为y=340-5(x-22)=-5x+450.
联立两线段所表示的函数关系式成方程组,
得$\left\{\begin{array}{l}{y=20x}\\{y=-5x+450}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=18}\\{y=360}\end{array}\right.$,
∴交点D的坐标为(18,360),
∴y与x之间的函数关系式为y=$\left\{\begin{array}{l}{20x(0≤x≤18)}\\{-5x+450(18<x≤30)}\end{array}\right.$.
(3)当0≤x≤18时,根据题意得:(8-6)×20x≥640,
解得:x≥16;
当18<x≤30时,根据题意得:(8-6)×(-5x+450)≥640,
解得:x≤26.
∴16≤x≤26.
26-16+1=11(天),
∴日销售利润不低于640元的天数共有11天.
∵点D的坐标为(18,360),
∴日最大销售量为360件,
360×2=720(元),
∴试销售期间,日销售最大利润是720元.
点评 本题考查了一次函数的应用、待定系数法一次函数解析式以及解一元一次不等式,解题的关键是:(1)根据数量关系,列式计算;(2)利用待定系数法求出OD的函数关系式以及依照数量关系找出DE的函数关系式;(3)分0≤x≤18和18<x≤30,找出关于x的一元一次不等式.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案| 污水处理器型号 | A型 | B型 |
| 处理污水能力(吨/月) | 240 | 180 |
(1)求每台A型、B型污水处理器的价格;
(2)为确保将每月产生的污水全部处理完,该企业决定购买上述的污水处理器,那么他们至少要支付多少钱?
 某几何体的左视图如图所示,则该几何体不可能是( )
某几何体的左视图如图所示,则该几何体不可能是( )| A. |  | B. |  | C. |  | D. |  |
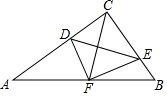 如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为$\frac{25}{8}$.
如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为$\frac{25}{8}$.
 在如图所示的两处各留1m宽的门,其余部分(不包括门)用篱笆围成.已知可用篱笆总长为18m,则能建成的矩形菜园占地面积最大为50m2.
在如图所示的两处各留1m宽的门,其余部分(不包括门)用篱笆围成.已知可用篱笆总长为18m,则能建成的矩形菜园占地面积最大为50m2.