题目内容
 在△ABC中,AB=AC,点E,F分别在AB,AC上,∠AEC=∠AFB,BF与CE相交于点P
在△ABC中,AB=AC,点E,F分别在AB,AC上,∠AEC=∠AFB,BF与CE相交于点P(1)求证:PB=PC,
(2)直接写出图中其他相等的线段(AE=AF除外).
考点:全等三角形的判定与性质,等腰三角形的性质
专题:计算题
分析:(1)利用AAS得到三角形ABF与三角形ACE全等,利用全等三角形对应角相等得到∠ABF=∠ACE,由AB=AC,利用等边对等角得到一对角相等,利用等式的性质得到∠PBC=∠PCB,根据等角对等边即可得证;
(2)由(1)的结论得到BF=CE,PE=PF,BE=CF.
(2)由(1)的结论得到BF=CE,PE=PF,BE=CF.
解答:(1)证明:∵AB=AC,
∴∠ABC=∠ACB,
在△ABF和△ACE中,
,
∴△ABF≌△ACE(AAS),
∴∠ABF=∠ACE,
∴∠ABC-∠ABF=∠ACB-∠ACE,即∠PBC=∠PCB,
∴PB=PC;
(2)解:相等的线段还有BF=CE,PF=PE,BE=CF.
∴∠ABC=∠ACB,
在△ABF和△ACE中,
|
∴△ABF≌△ACE(AAS),
∴∠ABF=∠ACE,
∴∠ABC-∠ABF=∠ACB-∠ACE,即∠PBC=∠PCB,
∴PB=PC;
(2)解:相等的线段还有BF=CE,PF=PE,BE=CF.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
已知a、b都是有理数,且|a|=a,|b|=-b,则ab是( )
| A、负数 | B、正数 |
| C、非正数 | D、非负数 |
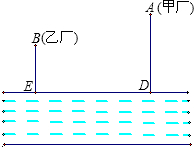 如图,大江的一侧有甲、乙两家工厂,它们都有垂直于江边的小路,长度分别为m千米和n千米,两条小路相距l千米.现在要在江边建一个抽水站,把水送到甲、乙两厂去.欲使供水管路最短,抽水站应建在哪里?
如图,大江的一侧有甲、乙两家工厂,它们都有垂直于江边的小路,长度分别为m千米和n千米,两条小路相距l千米.现在要在江边建一个抽水站,把水送到甲、乙两厂去.欲使供水管路最短,抽水站应建在哪里? 如图,点M把线段AB分成
如图,点M把线段AB分成 如图,在△ABC中,∠B=∠C,AD是BC边上的中线,E是AC上一点且DE=AE,求证:DE∥AB.
如图,在△ABC中,∠B=∠C,AD是BC边上的中线,E是AC上一点且DE=AE,求证:DE∥AB. 在同圆中,若
在同圆中,若
