题目内容
 在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE垂直平分线段AB.
在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE垂直平分线段AB.(1)求∠A;
(2)若DE=2cm,BD=4cm,求AC的长.
考点:线段垂直平分线的性质,角平分线的性质
专题:
分析:(1)先根据线段垂直平分线的性质得出AD=BD,故∠A=∠DBE.再根据BD平分∠ABC可知∠CBD=∠DBE.由∠C=90°,∠A=∠DBE=∠CBD可得出结论;
(2)先由角平分线的性质求出CD的长,再根据线段垂直平分线的性质得出AD的长,由此可得出结论.
(2)先由角平分线的性质求出CD的长,再根据线段垂直平分线的性质得出AD的长,由此可得出结论.
解答:
解:(1)∵DE是线段AB的垂直平分线,
∴AD=BD,
∴∠A=∠DBE.
∵BD平分∠ABC,
∴∠CBD=∠DBE.
∵∠C=90°,
∴∠A=∠DBE=∠CBD,
∴∠A=30°;
(2)∵∠C=90°,
∴DC⊥BC,
∵DE⊥BA,BD平分∠ABC,DE=DC=2cm,
∴BD=AD=4cm,
∴AC=AD+DC=6cm.
∴AD=BD,
∴∠A=∠DBE.
∵BD平分∠ABC,
∴∠CBD=∠DBE.
∵∠C=90°,
∴∠A=∠DBE=∠CBD,
∴∠A=30°;
(2)∵∠C=90°,
∴DC⊥BC,
∵DE⊥BA,BD平分∠ABC,DE=DC=2cm,
∴BD=AD=4cm,
∴AC=AD+DC=6cm.
点评:本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
小亮在“五一”假期间,为宣传“摈弃不良习惯,治理清江污染”的环保意识,对到利川市清江流域游玩人群的垃圾处理习惯(A带回处理、B焚烧掩埋、C就地扔掉,三者任选其一)进行了随机抽样调查.小亮根据调查情况进行统计,绘制的扇形统计图和频数分布直方图尚不完整,如图示.请结合统计图中的信息判断,下列说法错误的是( )


| A、抽样调查的样本数据是240 |
| B、“A带回处理”所在扇形的圆心角为18° |
| C、样本中“C就地扔掉”的人数是168 |
| D、样本中“B焚烧掩埋”的人数占“五一”假到利川市清江流域游玩人数的25% |
下列一元二次方程中,无实数根的是( )
| A、x2-2x+1=0 |
| B、2x2+3x+1=0 |
| C、x2+x-1=0 |
| D、x2-x+1=0 |
 大小相同的小正方体搭成的几何体从上面看到的图形如图所示,其中正方形中的数字表上的小正方体的个数,请你画出这个几何体从正面和左面看到的图形.
大小相同的小正方体搭成的几何体从上面看到的图形如图所示,其中正方形中的数字表上的小正方体的个数,请你画出这个几何体从正面和左面看到的图形.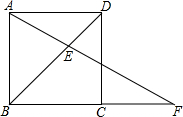 如图,已知E是正方形ABCD的对角线BD的黄金分割点(BE>DE),AE,BC的延长线交于F.若AB=2,求CF的长.
如图,已知E是正方形ABCD的对角线BD的黄金分割点(BE>DE),AE,BC的延长线交于F.若AB=2,求CF的长. 如图,直线AB∥CD,EG交CD于点G,EF⊥CD,F为垂足.若∠GEF=20°,则∠1=
如图,直线AB∥CD,EG交CD于点G,EF⊥CD,F为垂足.若∠GEF=20°,则∠1=