Question

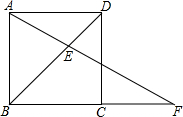如图，已知E是正方形ABCD的对角线BD的黄金分割点（BE＞DE），AE，BC的延长线交于F．若AB=2，求CF的长．

Answer 1

考点：黄金分割

专题：

分析：先由黄金分割的定义可得

DE

BE

=

5 -1

2

，然后由正方形性质可得AD∥BF，进而可得△ADE∽△FBE，然后由相似三角形的对应边成比例，可得：

AD

BF

=

DE

BE

=

5 -1

2

，然后由AD=AB=BC=2，代入即可求出CF的长．

解答： 解：∵E是正方形ABCD的对角线BD的黄金分割点（BE＞DE），
∴

DE

BE

=

5 -1

2

，
∵四边形ABCD是正方形，
∴AD∥BC，AD=BC=AB=2，
∴△ADE∽△FBE，
∴

AD

BF

=

DE

BE

=

5 -1

2

，
即：

2

2+CF

=

5 -1

2

，
解得：CF=

5

-1．

点评：此题考查了正方形的性质和黄金分割，相似三角形的判定和性质，难度中等，解题的关键是：熟记黄金比为

5 -1

2

．