题目内容
如图,直线 与x轴、y 轴分别交于点A 和点B,点C在直线AB上,且点C的纵坐标为一1,点D 在反比例函数
与x轴、y 轴分别交于点A 和点B,点C在直线AB上,且点C的纵坐标为一1,点D 在反比例函数 的图象上,CD平行于y轴,
的图象上,CD平行于y轴, ,则k的值为 。
,则k的值为 。
3
解析试题分析:把x=2代入 求出C的纵坐标,得出OM=2,CM=1,根据CD∥y轴得出D的横坐标是2,根据三角形的面积求出CD的值,求出MD,得出D的纵坐标,把D的坐标代入反比例函数的解析式求出k即可.
求出C的纵坐标,得出OM=2,CM=1,根据CD∥y轴得出D的横坐标是2,根据三角形的面积求出CD的值,求出MD,得出D的纵坐标,把D的坐标代入反比例函数的解析式求出k即可.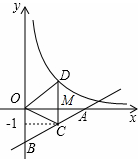
∵点C在直线AB上,即在直线 上,点C的纵坐标为-1,
上,点C的纵坐标为-1,
∴代入得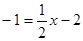 ,解得,x=2,即C(2,-1),
,解得,x=2,即C(2,-1),
∴OM=2,
∵CD∥y轴,S△OCD=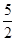 ,
,
∴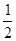 CD×OM=
CD×OM=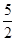 ,
,
∴CD=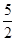 ,
,
∴MD=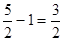 ,
,
即D的坐标是(2,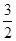 ),
),
∵D在双曲线 上,
上,
∴代入得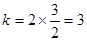 .
.
考点:反比例函数与一次函数的交点问题,一次函数、反比例函数的图象上点的坐标特征,三角形的面积公式
点评:通过做此题培养了学生的计算能力和理解能力,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
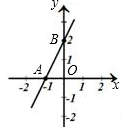 如图,直线与x轴、y轴分别交于A、B两点.
如图,直线与x轴、y轴分别交于A、B两点.
 3、如图,直线与y轴的交点是(0,-3),则当x<0时,( )
3、如图,直线与y轴的交点是(0,-3),则当x<0时,( ) 如图,直线与x轴、y轴分别交于A、B两点.
如图,直线与x轴、y轴分别交于A、B两点. 与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且
与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且 ,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.
,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.