题目内容
 如图,直线与x轴、y轴分别交于A、B两点.
如图,直线与x轴、y轴分别交于A、B两点.(1)将直线AB绕原点O沿逆时针方向旋转90°得到直线A1B1.请在《答题卡》所给的图中画出直线A1B1,此时直线AB与A1B1的位置关系为
垂直
垂直
(填“平行”或“垂直”)(2)设(1)中的直线AB的函数表达式为y1=k1x+b1,直线A1B1的函数表达式为y2=k2x+b2,则k1•k2=
-1
-1
.分析:(1)直线AB绕原点O沿逆时针方向旋转90°,即是直线上各点绕原点O沿逆时针方向旋转90°,由此得到A1B1点,由图象看出两直线垂直;
(2)分别求出两直线的函数表达式,得出k1•k2的值.
(2)分别求出两直线的函数表达式,得出k1•k2的值.
解答:解:(1)如图所示,

此时直线AB与A1B1的位置关系为垂直.故填:垂直;
(2)由图中图象得到直线AB的函数表达式y=2x+2
直线A1B1的函数表达式y=-
x-1
则k1•k2=-1.
故填:-1.

此时直线AB与A1B1的位置关系为垂直.故填:垂直;
(2)由图中图象得到直线AB的函数表达式y=2x+2
直线A1B1的函数表达式y=-
| 1 |
| 2 |
则k1•k2=-1.
故填:-1.
点评:本题考查了一次函数图象与几何变换.互相垂直的两条直线的斜率的乘积等于-1.

练习册系列答案
相关题目
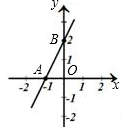 如图,直线与x轴、y轴分别交于A、B两点.
如图,直线与x轴、y轴分别交于A、B两点.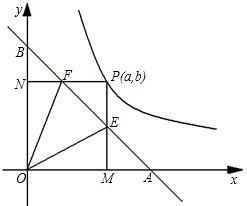
 3、如图,直线与y轴的交点是(0,-3),则当x<0时,( )
3、如图,直线与y轴的交点是(0,-3),则当x<0时,( ) 与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且
与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且 ,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.
,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.