��Ŀ����
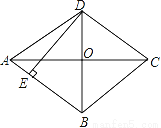
�ı���ABCD��ƽ���ı��Σ��Խ���ACƽ�֡�DAB��AC��BD�ཻ�ڵ�O��DE��AB��E�㣮��1����֤���ı���ABCD�����Σ�
��2����AC=8��BD=6����DE�ij��ȣ�
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
�ı���ABCD��ƽ���ı��Σ��Խ���ACƽ�֡�DAB��AC��BD�ཻ�ڵ�O��DE��AB��E�㣮��1����֤���ı���ABCD�����Σ�
��2����AC=8��BD=6����DE�ij��ȣ�
