题目内容
18.在直角坐标系中,一条直线经过A(-1,5),P(-2,a),B(3,-3)三点.(1)求a的值;
(2)设这条直线与y轴相交于点D,求△OPD的面积.
分析 (1)利用待定系数法解答解析式即可;
(2)得出直线与y轴相交于点D的坐标,再利用三角形面积公式解答即可.
解答 解:(1)设直线的解析式为y=kx+b,把A(-1,5),B(3,-3)代入,
可得:$\left\{\begin{array}{l}{-k+b=5}\\{3k+b=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=3}\end{array}\right.$,
所以直线解析式为:y=-2x+3,
把P(-2,a)代入y=-2x+3中,
得:a=7;
(2)由(1)得点P的坐标为(-2,7),
令x=0,则y=3,
所以直线与y轴的交点坐标为(0,3),
所以△OPD的面积=$\frac{1}{2}×3×2=3$.
点评 此题考查一次函数问题,关键是根据待定系数法解解析式.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
3.函数y=$\frac{\sqrt{x}}{x-1}$中,自变量的取值范围是( )
| A. | x≥0 | B. | x≠1 | C. | x>1 | D. | x≥0,且x≠1 |
10.一组数据x1,x2,x3,…,xn的平均数是a,方差是b,那么数据2x1,2x2,2x3…2xn的平均数和方差分别是( )
| A. | 2a和2b | B. | 2a和4b | C. | 4a和2b | D. | 4a和4b |
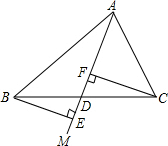 如图,射线AM与△ABC的BC边交于点D,BE⊥AM,CF⊥AM,垂足分别为E,F,当点D在什么位置时,BE=CF?请说明理由.(推理时不需要写出每一步的理由).
如图,射线AM与△ABC的BC边交于点D,BE⊥AM,CF⊥AM,垂足分别为E,F,当点D在什么位置时,BE=CF?请说明理由.(推理时不需要写出每一步的理由).