题目内容
5.先化简,再求值:(a-3-$\frac{7}{a+3}$)÷$\frac{a-4}{2a+6}$,其中a=$\sqrt{3}$-4.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把a的值代入计算即可求出值.
解答 解:原式=$\frac{{a}^{2}-9-7}{a+3}$•$\frac{2(a+3)}{a-4}$
=$\frac{(a+4)(a-4)}{a+3}$•$\frac{2(a+3)}{a-4}$
=2(a+4)
=2a+8,
当a=$\sqrt{3}$-4时,原式=2 ($\sqrt{3}$-4)+8=2$\sqrt{3}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
15. 如图,直线l1∥l2,∠2=65°,∠3=60°,则∠1为( )
如图,直线l1∥l2,∠2=65°,∠3=60°,则∠1为( )
 如图,直线l1∥l2,∠2=65°,∠3=60°,则∠1为( )
如图,直线l1∥l2,∠2=65°,∠3=60°,则∠1为( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |
20.在已知实数-1,0,$\frac{1}{2}$,-$\sqrt{3}$,20150中,最小的一个实数是( )
| A. | -$\sqrt{3}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 0 |
10.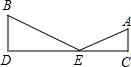 如图,球从A处射击,经过台边挡板CD反击,击中球B;已知AC=10cm,BD=15cm,CD=50cm,则点E距点C的距离是( )
如图,球从A处射击,经过台边挡板CD反击,击中球B;已知AC=10cm,BD=15cm,CD=50cm,则点E距点C的距离是( )
 如图,球从A处射击,经过台边挡板CD反击,击中球B;已知AC=10cm,BD=15cm,CD=50cm,则点E距点C的距离是( )
如图,球从A处射击,经过台边挡板CD反击,击中球B;已知AC=10cm,BD=15cm,CD=50cm,则点E距点C的距离是( )| A. | 20cm | B. | 30cm | C. | 15cm | D. | 35cm |
 如图,矩形ABCD是由三个矩形拼接成的.如果AB=8,阴影部分的面积是24,另外两个小矩形全等,那么小矩形的长为( )
如图,矩形ABCD是由三个矩形拼接成的.如果AB=8,阴影部分的面积是24,另外两个小矩形全等,那么小矩形的长为( )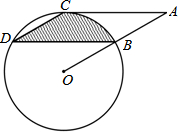 如图,点B,C,D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,BD=4$\sqrt{3}$,则由弦CD,BD与弧BC所围成的阴影部分的面积是$\frac{8}{3}$π.(结果保留π)
如图,点B,C,D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,BD=4$\sqrt{3}$,则由弦CD,BD与弧BC所围成的阴影部分的面积是$\frac{8}{3}$π.(结果保留π) 中国“蛟龙”号深潜器目前最大测潜极限为7062.68米,某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.
中国“蛟龙”号深潜器目前最大测潜极限为7062.68米,某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°. 我们知道,直角三角形的边角关系可用三角函数来描述,那么在任意三角形中,边角之间是否也存在某种关系呢?如图,锐角△ABC中,点A、B、C所对的边分别为a、b、c,过点C作CD⊥AB,在Rt△ADC中,CD=bsinA,AD=bcosA
我们知道,直角三角形的边角关系可用三角函数来描述,那么在任意三角形中,边角之间是否也存在某种关系呢?如图,锐角△ABC中,点A、B、C所对的边分别为a、b、c,过点C作CD⊥AB,在Rt△ADC中,CD=bsinA,AD=bcosA