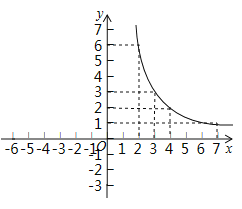题目内容
【题目】菱形![]() 的顶点C与原点O重合,点B落在y轴正半轴上,点A、D落在第一象限内,且D点坐标为
的顶点C与原点O重合,点B落在y轴正半轴上,点A、D落在第一象限内,且D点坐标为![]() .
.
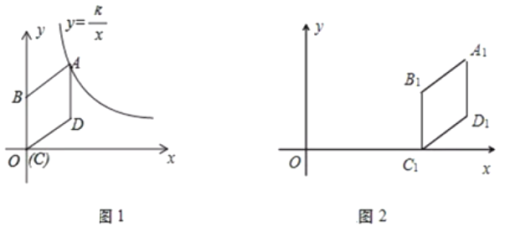
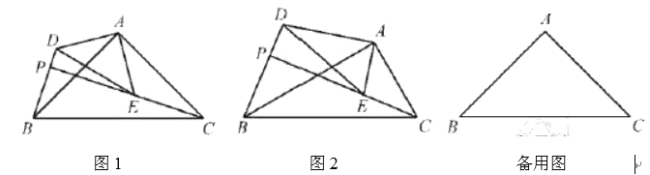
(1)如图1,若反比例函数![]() (
(![]() )的图象经过点A,求k的值;
)的图象经过点A,求k的值;
(2)菱形![]() 向右平移t个单位得到菱形
向右平移t个单位得到菱形![]() ,如图2.
,如图2.
①请直接写出点![]() 、
、![]() 的坐标(用合1的代数式表示):
的坐标(用合1的代数式表示):![]() 、
、![]() ;
;
②是否存在反比例函数![]() (
(![]() ),使得点
),使得点![]() 、
、![]() 同时落在
同时落在![]() (
(![]() )的图象上?若存在,求n的值;若不存在,请说明理由.
)的图象上?若存在,求n的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ,
,![]() ; ②存在,理由见解析
; ②存在,理由见解析
【解析】
(1)根据点D的坐标为(4,3),即可得出DE的长以及DO的长,即可得出A点坐标,进而求出k的值;
(2)①根据点向右平移,纵坐标不变,横坐标加上移动单位长即可;②把写出点![]()
![]() 、
、![]()
![]() 坐标代入
坐标代入![]() ,可得关于n、t的方程组,求解即可.
,可得关于n、t的方程组,求解即可.
(1)如图,作![]() 轴于点F,
轴于点F,

∵点D的坐标为![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∴A点坐标为![]()
∴![]() ,
,
∴![]() .
.
(2)①![]() ,
,![]()
②存在,理由如下:
∵点![]() 、
、![]() 同时落在
同时落在![]() (
(![]() )的图象上
)的图象上
![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
![]()
![]()
所以,存在,此时![]() .
.

练习册系列答案
相关题目
【题目】小楠是一个乐学习,善思考,爱探究的同学,她对函数![]() 的图象和性质进行了探究,请你将下列探究过程补充完整:
的图象和性质进行了探究,请你将下列探究过程补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是________________;
的取值范围是________________;
(2)用描点法画函数图象:
①列表:
| … | -5 | -2 | -1 | 0 | … | 2 | 3 | 4 | 7 | … |
| … |
| 2 | 3 |
| … | 6 | 3 | 2 | 1 | … |
表中![]() 的值为______________,
的值为______________,![]() 的值为_______________.
的值为_______________.
②描点连线:请在右图画出该图象的另一部分.
(3)观察函数图象,得到函数![]() 的性质之一:当
的性质之一:当![]() _____________时,函数值
_____________时,函数值![]() 随
随![]() 的增大而增大.
的增大而增大.
(4)应用:若![]() ,则
,则![]() 的取值范围是______________.
的取值范围是______________.