题目内容
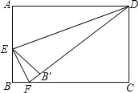
【题目】（问题实验）如图①，在地面
上有两根等长立柱
，
之间悬挂一根近似成抛物线
的绳子．
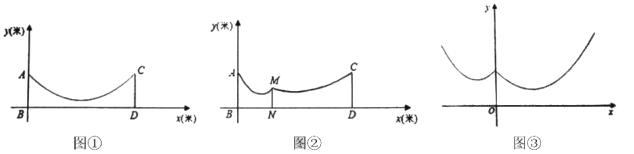
（1）求绳子最低点到地面的距离；
（2）如图②，因实际需要，需用一根立柱
撑起绳子．
①若在离为4米的位置处用立柱撑起，使立柱左侧的抛物线的最低点距为1米，离地面1.8米，求的长；
②将立柱来回移动，移动过程中，在一定范围内，总保持立柱左侧抛物线的形状不变，其函数表达式为
，当抛物线最低点到地面距离为0.5米时，求
的值．
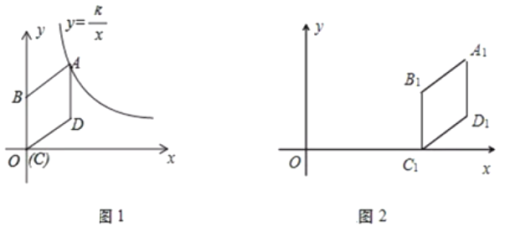
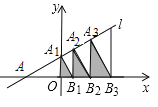
（问题抽象）如图③，在平面直角坐标系中，函数
的图像记为
，函数
的图像记为
，其中是常数，图像、合起来得到的图像记为
．
设在
上的最低点纵坐标为
，当
时，直接写出的取值范围．
【答案】【问题实验】（1）
米；（2）①
米；②
；【问题抽象】
或
．
【解析】
【问题实验】
（1）先把抛物线转化为顶点式，进而可得答案；
（2）①先求出点A坐标，由题意可设
，然后把点A坐标代入即可求出a的值，再求当x=4时对应的y的值即为所求；
②根据题意可确定：该抛物线的顶点坐标为
，然后把该点代入抛物线的解析式可得关于m的方程，解方程并结合抛物线对称轴的位置即可求出结果；
【问题抽象】
当
时，对
，确定其对称轴为直线
后，由于
，可分
与
两种情况，根据抛物线的性质确定其最小值y0，然后由
即可得到关于m的不等式组，解不等式组即可求出结果；当x＜0时，对于
，确定其对称轴是直线x=m后，仿照上面的思路求解即可．
解：【问题实验】（1）
，
∴绳子最低点到地面的距离是米；
（2）对
，当x=0时，y=3，∴A（0，3），
①由题意可知：MN左侧的抛物线的顶点为（3，1.8），于是设抛物线的解析式为，
把
代入，得：
，解得：
，
∴
，
当
时，
，
∴米；
②由于的对称轴是直线x=m，所以该抛物线的顶点坐标为，
把代入中，
，
解得：
，
，
由于抛物线的对称轴在y轴右侧，∴；
【问题抽象】
由题意知：抛物线M1、M2均过定点（0，3），当m≥0时，M1的最低点为（0，3），此时，抛物线M的最低点在M2上．当时，对M2：，其对称轴是直线．
①当，即
时，
∵当时，y随x的增大而减小，∴当x=2时，y最小，此时
，
∵，∴
，解得：；
②当，即
时，
∵x的范围是，∴当x=2m时y最小，此时
，
∵，∴
，解得：
，
∵，∴此种情况的m的值不存在；
当m＜0时，M2的最低点为（0，3），此时，抛物线M的最低点在M1上，当x＜0时，对于M1：，其对称轴是直线x=m．
③当
时，
∵当
时，y随x的增大而增大，∴当x=﹣3时，y最小，此时
，
∵，∴
，解得：
，
∵，所以m的范围是
；
④当
时，
∵x的范围是，∴当x=m时，y最小，此时
，
∵，∴
，解得：
，
∵，∴
；
综上所述，m的取值范围是：或．
