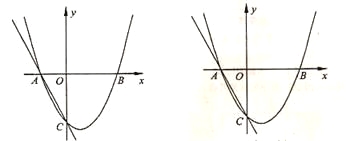题目内容
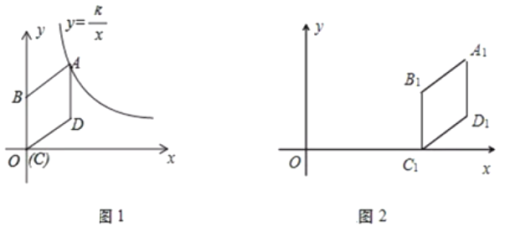
【题目】已知抛物线![]()
![]() 的图象与x轴交于A,B两点,与y轴交于点C,且关于直线
的图象与x轴交于A,B两点,与y轴交于点C,且关于直线![]() 对称,点A的坐标为(﹣1,0).
对称,点A的坐标为(﹣1,0).
(Ⅰ)求抛物线C的解析式和顶点坐标;
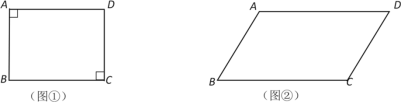
(Ⅱ)将抛物线![]() 绕点O顺时针旋转180°得抛物线
绕点O顺时针旋转180°得抛物线![]() ,且有点P(m,t)既在抛物线
,且有点P(m,t)既在抛物线![]() 上,也在抛物线
上,也在抛物线![]() 上,求m的值;
上,求m的值;
(Ⅲ)当![]() 时,二次函数
时,二次函数![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)y=x2﹣2x﹣3;顶点坐标为(1,-4);(Ⅱ)![]() ,
,![]() ;(Ⅲ)a的值为1﹣
;(Ⅲ)a的值为1﹣![]() 或2+
或2+![]() .
.
【解析】
(1)利用二次函数的对称性,由![]() 点坐标得出
点坐标得出![]() 点坐标,利用二次函数的交点式直接写出解析式即可,把二次函数的化成顶点式,直接求出顶点坐标;
点坐标,利用二次函数的交点式直接写出解析式即可,把二次函数的化成顶点式,直接求出顶点坐标;
(2)先求出抛物线![]() 的解析式,把
的解析式,把![]() 分别代入到
分别代入到![]() 、
、![]() 的解析式中得到关于
的解析式中得到关于![]() 的方程组,解方程组即可得出正确答案;
的方程组,解方程组即可得出正确答案;
(3)分![]() 、
、![]() 、
、![]() 三种情况讨论即可.
三种情况讨论即可.
解:(Ⅰ)∵点A(﹣1,0)与点B关于直线x=1对称,
∴点B的坐标为(3,0),
则![]() ,
,
即抛物线C的表达式为y=x2﹣2x﹣3;
∵![]() ,
,
∴ 顶点坐标为![]() .
.
(Ⅱ)由抛物线C解析式知B(3,0),点A的坐标为(﹣1,0)
所以点A点B关于原点的对称点为(1,0)和(﹣3,0),都在抛物线![]() 上,
上,
且抛物线![]() 开口向下,形状与由抛物线C相同,
开口向下,形状与由抛物线C相同,
于是可得抛物线![]() 的解析式为
的解析式为![]() ,即y=﹣x2﹣2x+3;
,即y=﹣x2﹣2x+3;
由点![]() 在抛物线
在抛物线![]() 上,有
上,有![]() ,
,
由点![]() 也在抛物线
也在抛物线![]() 上,有
上,有![]() ,
,
∴![]() .
.
解得![]() ,
,![]() .
.
(III)①当a+1<1时,即a<0,
则函数的最小值为(a+1)2﹣2(a+1)﹣3=2a,
解得a=1﹣![]() (正值舍去);
(正值舍去);
②当a<1≤a+1时,即0≤a<1,
则函数的最小值为1﹣2﹣3=2a,
解得:a=﹣2(舍去);
③当![]() 时,
时,
则函数的最小值为a2﹣2a﹣3=2a,解得a=2+![]() (负值舍去);
(负值舍去);
综上,a的值为1﹣![]() 或2+
或2+![]() .
.

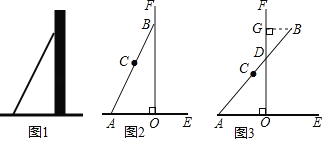
【题目】数学活动课上,张老师引导同学进行如下探究:如图1,将长为![]() 的铅笔
的铅笔![]() 斜靠在垂直于水平桌面
斜靠在垂直于水平桌面![]() 的直尺
的直尺![]() 的边沿上,一端
的边沿上,一端![]() 固定在桌面上,图2是示意图.
固定在桌面上,图2是示意图.
活动一
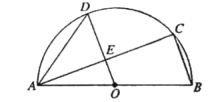
如图3,将铅笔![]() 绕端点
绕端点![]() 顺时针旋转,
顺时针旋转,![]() 与
与![]() 交于点
交于点![]() ,当旋转至水平位置时,铅笔
,当旋转至水平位置时,铅笔![]() 的中点
的中点![]() 与点
与点![]() 重合.
重合.
数学思考
(1)设![]() ,点
,点![]() 到
到![]() 的距离
的距离![]() .
.
①用含![]() 的代数式表示:
的代数式表示:![]() 的长是_________
的长是_________![]() ,
,![]() 的长是________
的长是________![]() ;
;
②![]() 与
与![]() 的函数关系式是_____________,自变量
的函数关系式是_____________,自变量![]() 的取值范围是____________.
的取值范围是____________.
活动二
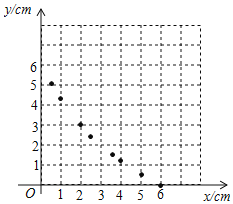
(2)①列表:根据(1)中所求函数关系式计算并补全表格.
| 6 | 5 | 4 | 3.5 | 3 | 2.5 | 2 | 1 | 0.5 | 0 |
| 0 | 0.55 | 1.2 | 1.58 | 1.0 | 2.47 | 3 | 4.29 | 5.08 |
②描点:根据表中数值,描出①中剩余的两个点![]() .
.
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考
(3)请你结合函数的图象,写出该函数的两条性质或结论.