题目内容
13.设正n边形的半径为R,边心距为r,如果我们将$\frac{R}{r}$的值称为正n边形的“接近度”,那么正六边形的“接近度”是$\frac{{2\sqrt{3}}}{3}$(结果保留根号).分析 求出正六边形的边心距(用R表示),根据“接近度”的定义即可解决问题.
解答 解:∵正六边形的半径为R,
∴边心距r=$\frac{\sqrt{3}}{2}$R,
∴正六边形的“接近度”=$\frac{R}{r}$=$\frac{R}{\frac{\sqrt{3}}{2}R}$=$\frac{2\sqrt{3}}{3}$.
故答案为$\frac{2\sqrt{3}}{3}$.
点评 本题考查正多边形与圆的共线,等边三角形高的计算,记住等边三角形的高h=$\frac{\sqrt{3}}{2}$a(a是等边三角形的边长),理解题意是解题的关键,属于中考常考题型.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
3.因式分解x2-4的结果是( )
| A. | x(x-4) | B. | x(x-2)2 | C. | (x-2)(x+2) | D. | x(x+2)2 |
1.崇明县校园足球运动正在蓬勃发展,已知某校学生“足球社团”成员的年龄与人数情况如下表所示:那么“足球社团”成员年龄的中位数是14岁.
| 年龄(岁) | 11 | 12 | 13 | 14 | 15 |
| 人数 | 3 | 3 | 7 | 12 | 14 |
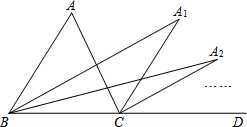 如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…∠An-1BC的平行线与∠An-1CD的平分线交于点An,设∠A=θ,则∠An=$\frac{θ}{{2}^{n}}$.
如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…∠An-1BC的平行线与∠An-1CD的平分线交于点An,设∠A=θ,则∠An=$\frac{θ}{{2}^{n}}$.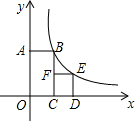 如图,四边形OABC是矩形,四边形CDEF是正方形,点C,D在x轴的正半轴上,点A在y轴的正半轴上,点F在BC上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=2,OC=1,则正方形CDEF的面积为( )
如图,四边形OABC是矩形,四边形CDEF是正方形,点C,D在x轴的正半轴上,点A在y轴的正半轴上,点F在BC上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=2,OC=1,则正方形CDEF的面积为( )