题目内容
9.(1)(2$\sqrt{5}$)2;(2)$\sqrt{8}$+2$\sqrt{3}$-($\sqrt{27}$-$\sqrt{2}$);
(3)$\sqrt{\frac{2}{3}}$+$\sqrt{2\frac{2}{3}}$×$\sqrt{\frac{2}{5}}$;
(4)($\sqrt{5}$+$\sqrt{6}$)($\sqrt{5}$-$\sqrt{6}$)
分析 (1)利用二次根式化的性质计算即可;
(2)先把二次根式化为最简二次根式,然后合并即可;
(3)先进行二次根式化的乘法运算,然后化简即可;
(4)利用平方差公式计算.
解答 解:(1)原式=4×5=20;
(2)原式=2$\sqrt{2}$+2$\sqrt{3}$-3$\sqrt{3}$+$\sqrt{2}$
=3$\sqrt{2}$-$\sqrt{3}$;
(3)原式=$\frac{\sqrt{6}}{3}$+$\sqrt{\frac{8}{3}×\frac{2}{5}}$
=$\frac{\sqrt{6}}{3}$+$\frac{4\sqrt{15}}{15}$;
(4)原式=5-6
=-1.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
4.抛物线y=-2(x+3)2是由抛物线y=-2x2向( )平移( )个单位得到的.
| A. | 左、3 | B. | 右、3 | C. | 上、3 | D. | 下、3 |
18.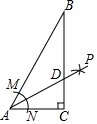 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,小于AC为半径画弧,分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连接AP交BC于点,则下列说法不正确的是( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,小于AC为半径画弧,分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连接AP交BC于点,则下列说法不正确的是( )
 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,小于AC为半径画弧,分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连接AP交BC于点,则下列说法不正确的是( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,小于AC为半径画弧,分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连接AP交BC于点,则下列说法不正确的是( )| A. | AD平分∠BAC | B. | S△DAC:S△ABC=1:2 | ||
| C. | 点D在线段AB的垂直平分线上 | D. | ∠ADC=60° |
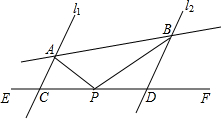 如图,已知直线l1∥l2,直线AB与l1,l2分别交于点A,B,直线EF与l1,l2分别交于点C,D,P是直线EF上的任意一点(不与点C,D重合).
如图,已知直线l1∥l2,直线AB与l1,l2分别交于点A,B,直线EF与l1,l2分别交于点C,D,P是直线EF上的任意一点(不与点C,D重合).
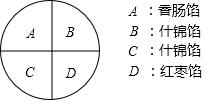 大年夜吃饺子是中华民族的传统习俗,妈妈为洋洋准备了四只饺子:一只香肠陷A,两只什锦馅B和C,一只红枣馅D,四只饺子除内部馅料不同外,其他均一切相同,洋洋喜欢吃什锦馅的饺子.
大年夜吃饺子是中华民族的传统习俗,妈妈为洋洋准备了四只饺子:一只香肠陷A,两只什锦馅B和C,一只红枣馅D,四只饺子除内部馅料不同外,其他均一切相同,洋洋喜欢吃什锦馅的饺子.