题目内容
1.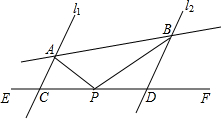 如图,已知直线l1∥l2,直线AB与l1,l2分别交于点A,B,直线EF与l1,l2分别交于点C,D,P是直线EF上的任意一点(不与点C,D重合).
如图,已知直线l1∥l2,直线AB与l1,l2分别交于点A,B,直线EF与l1,l2分别交于点C,D,P是直线EF上的任意一点(不与点C,D重合).(1)若∠PAC=62°,∠PBD=31°,则∠APB=93°或31°.
(2)探究∠PAC,∠APB,∠PBD之间的关系,可以得到的结论是∠APB=∠PAC+∠PBD或∠PAC=∠PBD+∠APB或∠PBD=∠PAC+∠APB.
分析 (1)分三种情况讨论:点P在CD之间时,点P在CD的延长线上,点P在DC延长线上,分别过P作PG∥AC,根据平行线的性质进行计算即可得到∠APB的度数;
(2)分三种情况讨论:点P在CD之间时,点P在CD的延长线上,点P在DC延长线上,分别过P作PG∥AC,根据平行线的性质进行推导,即可得到∠PAC,∠APB,∠PBD之间的关系.
解答 解:(1)当点P在CD之间时,过P作PG∥AC,则PG∥BD,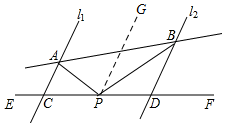
∴∠APG=∠PAC=62°,∠BPG=∠PBD=31°,
∴∠APB=∠APG+∠BPG=62°+31°=93°,
当点P在CD的延长线上时,过P作PG∥AC,则PG∥BD,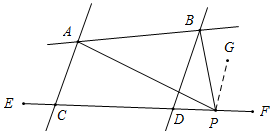
∴∠APG=∠PAC=62°,∠BPG=∠PBD=31°,
∴∠APB=∠APG-∠BPG=62°-31°=31°;
当点P在DC延长线上时,不合题意;
综上所述,∠APB=93°或31°,
故答案为:93°或31°;
(2)如图,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:过点P作PG∥l1,
∵l1∥l2,
∴PG∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
如图,当点P在CD延长线上时,∠PAC=∠PBD+∠APB.
理由如下:过点P作PG∥l1,
∵l1∥l2,
∴PG∥l2∥l1,
∴∠APG=∠PAC,∠BPG=∠PBD,
∵∠APG=∠BPG+∠APB,
∴∠PAC=∠PBD+∠APB.
如图,当点P在DC延长线上时,∠PBD=∠PAC+∠APB.
理由如下:过点P作PG∥l1,
∵l1∥l2,
∴PG∥l2∥l1,
∴∠APG=∠PAC,∠BPG=∠PBD,
∵∠BPG=∠APG+∠APB,
∴∠PBD=∠PAC+∠APB.
故答案为:∠APB=∠PAC+∠PBD或∠PAC=∠PBD+∠APB或∠PBD=∠PAC+∠APB.
点评 本题主要考查了平行线的性质,解题的关键是掌握:两直线平行,内错角相等,解题时注意辅助线的作法.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案 《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开放术、正负术和方程术.其中方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有共买鸡,人出八,盈三;人出七,不足四.问人数、鸡价各几何?”译文:“今天有几个人共同买鸡,每人出8钱,多余3钱,每人出7钱,还缺4钱.问人数和鸡的价钱各是多少?”设人数有x人,鸡的价钱是y钱,可列方程组为$\left\{\begin{array}{l}{8x-3=y}\\{7x+4=y}\end{array}\right.$.
《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开放术、正负术和方程术.其中方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有共买鸡,人出八,盈三;人出七,不足四.问人数、鸡价各几何?”译文:“今天有几个人共同买鸡,每人出8钱,多余3钱,每人出7钱,还缺4钱.问人数和鸡的价钱各是多少?”设人数有x人,鸡的价钱是y钱,可列方程组为$\left\{\begin{array}{l}{8x-3=y}\\{7x+4=y}\end{array}\right.$. 如图,l1∥l2∥l3若∠1=70°,∠2=50°,则∠ABC=120度.
如图,l1∥l2∥l3若∠1=70°,∠2=50°,则∠ABC=120度.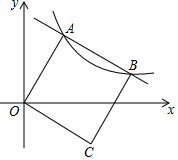 如图,平面直角坐标系中,O为坐标原点,正方形OABC的顶点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,边BC与x轴交于点D,则$\frac{BD}{CD}$的值为$\frac{\sqrt{5}-1}{2}$.
如图,平面直角坐标系中,O为坐标原点,正方形OABC的顶点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,边BC与x轴交于点D,则$\frac{BD}{CD}$的值为$\frac{\sqrt{5}-1}{2}$.