题目内容
4．填空：a=$\frac{1}{2}$，b=$\frac{1}{3}$，则$\frac{3{a}^{2}-ab}{3{a}^{2}+5ab-2{b}^{2}}$=$\frac{3}{7}$．分析 原式分子、分母分解因式后约分得到最简结果，将a与b的值代入计算即可求出值．
解答 解：原式=$\frac{a（3a-b）}{（3a-b）（a+2b}$
=$\frac{a}{a+2b}$；
当a=$\frac{1}{2}$，b=$\frac{1}{3}$时，原式=$\frac{\frac{1}{2}}{\frac{1}{2}+2×\frac{1}{3}}$=$\frac{3}{7}$．
故答案为$\frac{3}{7}$．
点评 此题考查了分式的化简求值，涉及的知识有：因式分解，分式的约分，熟练掌握因式分解法是解本题的关键．
练习册系列答案
相关题目
15．
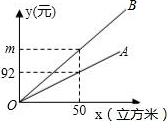某市发改委举行居民用水价格调整听证会，届时将有两个方案提供听证．如图，射线OA、射线OB分别表示现行的、方案一的每户每月的水费y（元）与每户每月的用水量x（立方米）之间的函数关系，已知方案一的用水价比现行的用水价每立方米多0.96元；
方案二如表所示，每月的每立方米用水价格由该月的用水量决定，其第一、二、三阶的用水价格之比为1：1.5：2（精确到0.01元）
（1）现行的用水量是每立方米1.84元，第三阶的用水价格a=5.22；
（2）求图中m的值和射线OB所对应的函数关系式；
（3）若小明家某月的用水量是a（立方米），请分别写出所提的两种方案下该月的水费b（元）【用含a的代数式表示】
某市发改委举行居民用水价格调整听证会，届时将有两个方案提供听证．如图，射线OA、射线OB分别表示现行的、方案一的每户每月的水费y（元）与每户每月的用水量x（立方米）之间的函数关系，已知方案一的用水价比现行的用水价每立方米多0.96元；方案二如表所示，每月的每立方米用水价格由该月的用水量决定，其第一、二、三阶的用水价格之比为1：1.5：2（精确到0.01元）
| 阶数 | 用水量（立方米） | 用水价格（元/立方米） |
| 第一阶 | 0～15（含15）的部分 | 2.61 |
| 第二阶 | 15～25（含25）的部分 | 3.92 |
| 第三阶 | 25以上的得分 | n |
（2）求图中m的值和射线OB所对应的函数关系式；
（3）若小明家某月的用水量是a（立方米），请分别写出所提的两种方案下该月的水费b（元）【用含a的代数式表示】
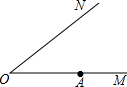如图，已知ON是一条公路桥梁，现要在上游点A处再建一座与ON平行的大桥AB，请用尺规画出AB方向（不必写作法）．并根据你的作法用一句话简单说明为什么AB和ON是平行的？
如图，AD⊥BC于点D，点E在边AB上，CE与AD交于点G，EF⊥AD于点F，AE=5cm，BE=10cm，BD=9cm，CD=5cm，求AF、FG、GD的长．
14．有6张写有数字的卡片，它们的背面都相同，现将它们背面朝上（如图所示），从中任意一张是数字1的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |