题目内容
9.已知关于x的方程(k-1)x2+(k-1)x+k-2=0有两个相等的实数根,则k的值是1或$\frac{7}{3}$.分析 若一元二次方程有两等根,则根的判别式△=b2-4ac=0,建立关于k的方程,求出k的取值.
解答 解:∵方程有两个相等的实数根,
∴△=0.
又∵△=(k-1)2-4(k-1)(k-2)=-3k2+10k-7,
∴-3k2+10k-7=0,
∴k=1或$\frac{7}{3}$,
故答案为1或$\frac{7}{3}$.
点评 本题考查了根的判别式,总结:一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
18. 随县炎帝神农大像底座边长56尺,意为中国56个民族,底座高度为42.6尺,意为炎帝神农诞生日农历四月二十六日;立像高为95尺(约34.670米),唐县镇七年级同学张婉秋在参观后问:“31.670米这个数有几个有效数字,精确到哪一位呢?”( )
随县炎帝神农大像底座边长56尺,意为中国56个民族,底座高度为42.6尺,意为炎帝神农诞生日农历四月二十六日;立像高为95尺(约34.670米),唐县镇七年级同学张婉秋在参观后问:“31.670米这个数有几个有效数字,精确到哪一位呢?”( )
 随县炎帝神农大像底座边长56尺,意为中国56个民族,底座高度为42.6尺,意为炎帝神农诞生日农历四月二十六日;立像高为95尺(约34.670米),唐县镇七年级同学张婉秋在参观后问:“31.670米这个数有几个有效数字,精确到哪一位呢?”( )
随县炎帝神农大像底座边长56尺,意为中国56个民族,底座高度为42.6尺,意为炎帝神农诞生日农历四月二十六日;立像高为95尺(约34.670米),唐县镇七年级同学张婉秋在参观后问:“31.670米这个数有几个有效数字,精确到哪一位呢?”( )| A. | 有4个有效数字,精确到千分位 | B. | 有3个有效数字,精确到万分位 | ||
| C. | 有5个有效数字,精确到千分位 | D. | 有3个有效数字,精确到十位 |
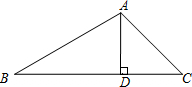 如图,在△ABC中,∠B=30°,∠C=45°,AC=2$\sqrt{2}$.求BC边上的高及△ABC的面积.
如图,在△ABC中,∠B=30°,∠C=45°,AC=2$\sqrt{2}$.求BC边上的高及△ABC的面积.