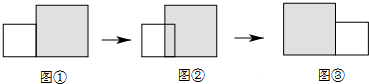
题目内容
12.正方形ABCD内有一点E,且△ABE为等边三角形,则∠DCE为( )| A. | 15° | B. | 18° | C. | 22.5° | D. | 30° |
分析 作出图形,根据正方形的四条边都相等,等边三角形的三条边都相等可得BC=BE=AB,再求出∠CBE=30°,然后根据等腰三角形两底角相等求出∠BCE,然后求解即可.
解答  解:如图,∵四边形ABCD是正方形,△ABE为等边三角形,
解:如图,∵四边形ABCD是正方形,△ABE为等边三角形,
∴BC=BE=AB,∠ABC=90°,∠ABE=60°,
∴∠CBE=90°-60°=30°,
∴∠BCE=$\frac{1}{2}$(180°-30°)=75°,
∴∠DCE=∠BCD-∠BCE=90°-75°=15°.
故选A.
点评 本题考查了正方形的性质,等边三角形的性质,熟记各性质并理清图中各角度之间的关系是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
19. 如图,由一些完全相同的小正方体搭成的几何体的俯视图和左视图,组成这个几何体的小正方体的个数是( )
如图,由一些完全相同的小正方体搭成的几何体的俯视图和左视图,组成这个几何体的小正方体的个数是( )
 如图,由一些完全相同的小正方体搭成的几何体的俯视图和左视图,组成这个几何体的小正方体的个数是( )
如图,由一些完全相同的小正方体搭成的几何体的俯视图和左视图,组成这个几何体的小正方体的个数是( )| A. | 5或6或7 | B. | 6或7 | C. | 6或7或8 | D. | 7或8或9 |

 如图,正方形ABCD中,E,F为边BC上的点,且BE=CF,连结BD,DE,过点C作CH⊥DE于G,交BD于H,连结FH
如图,正方形ABCD中,E,F为边BC上的点,且BE=CF,连结BD,DE,过点C作CH⊥DE于G,交BD于H,连结FH