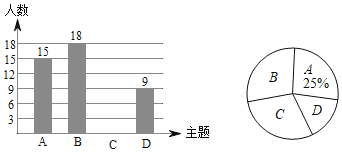
��Ŀ����
����Ŀ����ͼ���ڶ�������ĺ�����![]() �ϣ���
�ϣ���![]() ��
��![]() ����Ѳ�ߴ��۲��
����Ѳ�ߴ��۲��![]() ��
��![]() ��
��![]() ��
��![]() ��ֱ��
��ֱ��![]() �ϣ�������ͬʱ�յ��洬
�ϣ�������ͬʱ�յ��洬![]() �ں���ͣ�͵㷢��������źţ�����洬�ֱ���Ѳ�ߴ�
�ں���ͣ�͵㷢��������źţ�����洬�ֱ���Ѳ�ߴ�![]() ��
��![]() ��ƫ��
��ƫ��![]() �ͱ�ƫ��
�ͱ�ƫ��![]() ����Ѳ�ߴ�
����Ѳ�ߴ�![]() ���洬
���洬![]() ���120����洬�ڹ۲��
���120����洬�ڹ۲��![]() ��ƫ��
��ƫ��![]() ����˵�������ȡ�������ο����ݣ�
����˵�������ȡ�������ο����ݣ�![]() ��
��![]() ����
����
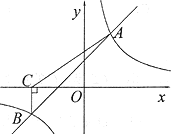
��1����Ѳ�ߴ�![]() ��۲��
��۲��![]() ��ľ��룻
��ľ��룻
��2����֪�۲��![]() ��45����ķ�Χ���а�������Ѳ�ߴ�
��45����ķ�Χ���а�������Ѳ�ߴ�![]() ��
��![]() ����ȥӪ���洬
����ȥӪ���洬![]() ��û�д�����Σ�գ���˵�����ɣ�
��û�д�����Σ�գ���˵�����ɣ�

���𰸡���1��76�����2��û�д�����Σ�գ����ɼ�����
��������
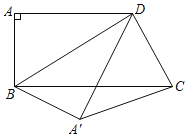
��1����![]() ������ֱ��������������AE��CE,AB����֤
������ֱ��������������AE��CE,AB����֤![]() ������
������![]() ��
��
��2����![]() ��֤BF=DF����BF2+DF2=BD2�����.
��֤BF=DF����BF2+DF2=BD2�����.
�⣺��1����![]() ��
��
��Ϊ�洬�ֱ���Ѳ�ߴ�![]() ��
��![]() ��ƫ��
��ƫ��![]() �ͱ�ƫ��
�ͱ�ƫ��![]() ����
����
���ԡ�CAE=60��, ��CBE=45��
���ԡ�ACE=30��, ��ACB=180��-60��-45��=75��;
����![]() �������
�������![]() �������
�������

����![]() ��
��
��Ϊ�洬�ڹ۲��![]() ��ƫ��
��ƫ��![]() ����
����
���ԡ�CDE=75
���ԡ�CDE=��ACB,
����![]() ��
��
����![]() ��
��
��![]() ��
��
��ã�![]() ��
��
��![]() ���
���
��2��û�д�����Σ�գ�
��![]() ��
��
����CBD=45��
����BF=DF
����BF2+DF2=BD2
��DF2+DF2=762
�����![]() ��
��
��![]() ��
��
��û�д�����Σ�գ�

��ϰ��ϵ�д�
�����Ŀ