化简或计算:(1)$\root{3}{-8}$-0+$\sqrt{4}$(2)$\frac{3}{2}$$\sqrt{18m}$•$\sqrt{2m}$+$\sqrt{72{m}^{3}}$÷$\sqrt{8m}$-2m．题目和参考答案——青夏教育精英家教网—

题目内容

15．化简或计算：
（1）$\root{3}{-8}$-（1+$\sqrt{3}$）⁰+$\sqrt{4}$
（2）$\frac{3}{2}$$\sqrt{18m}$•$\sqrt{2m}$+$\sqrt{72{m}^{3}}$÷$\sqrt{8m}$-2m．

分析（1）原式第一项利用立方根定义计算，第二项利用零指数幂法则计算，最后一项利用算术平方根计算即可得到结果；
（2）原式各项化简后，合并即可得到结果．

解答解：（1）原式=-2-1+2=-1；
（2）原式=9m+6m$\sqrt{2m}$÷2$\sqrt{2m}$-2m=9m+3m-2m=10m．

点评此题考查了实数的运算，熟练掌握运算法则是解本题的关键．

练习册系列答案

红对勾45分钟作业与单元评估系列答案

重难点手册系列答案

创维新课堂系列答案

世纪百通主体课堂小学课时同步达标系列答案

相关题目

$\sqrt{3}+\sqrt{4}=\sqrt{7}$

B．

$\sqrt{2}+\sqrt{5}=\sqrt{10}$

C．

$\sqrt{48}=4\sqrt{3}$

D．

2$\sqrt{6}-\sqrt{6}$=2

6．下列条件中，能作出唯一三角形的是（　　）

a²+a²=2a⁴

a⁵-a²=a³

10．若|x+1|+（y-2）²=0，则（x+y）²⁰¹⁵=1．

20．多项式3x²y-xy³+5xy-1是一个（　　）

7．计算：
（1）8+（-10）+（-2）+（-5）
（2）（+$\frac{1}{4}$）+（-2$\frac{1}{3}$）-（-2$\frac{3}{4}$）-（+3$\frac{2}{3}$）
（3）（$\frac{3}{8}$-$\frac{1}{6}$-$\frac{3}{4}$）×24
（4）-1⁶-|-5|+2×（-$\frac{1}{2}$）²．

4．

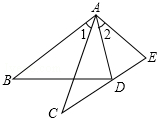如图，在△ABD和△ACE中，有下列四个等式：①AB=AC、②AD=AE、③∠1=∠2、④BD=CE．请你以其中三个等式作为题设，余下的作为结论，写出一个真命题（要求写出已知，求证及证明过程）题设：①②③，结论：④（写序号）

5．比较下列各组数的大小：
（1）$\sqrt{5}$-3，$\frac{\sqrt{5}-2}{2}$；
（2）$\sqrt{7}$-$\sqrt{6}$，$\sqrt{6}$-$\sqrt{5}$；
（3）-$\sqrt{6}$，-2$\sqrt{6}$；
（4）$\frac{\sqrt{2}}{2}$，$\frac{\sqrt{3}}{3}$．

试题分类