题目内容
若正六边形的边长为a，则其外接圆半径与内切圆半径的比为（ ）
| A、2：1 | ||
B、2：
| ||
C、
| ||
D、3：
|
考点：正多边形和圆
专题：
分析：从内切圆的圆心和外接圆的圆心向三角形的连长引垂线，构建直角三角形，解三角形即可．
解答：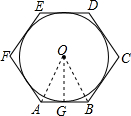
解：∵正六边形的边长为a，
∴正六边形的半径是a，
则外接圆的半径a，
内切圆的半径是正六边形的边心距，因而是GO=
a，
因而正六边形的外接圆的半径与内切圆的半径之比为2：
．
故选：B．
解：∵正六边形的边长为a，∴正六边形的半径是a，
则外接圆的半径a，
内切圆的半径是正六边形的边心距，因而是GO=
| ||
| 2 |
因而正六边形的外接圆的半径与内切圆的半径之比为2：
| 3 |
故选：B．
点评：此题主要考查了正多边形和圆，正多边形的计算一般是通过中心作边的垂线，连接半径，把正多边形中的半径，边长，边心距，中心角之间的计算转化为解直角三角形．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
广州市番禺区莲花山旅游区是旅游热点，每年的春节期间是旅游的旺季，在2013年的春节期间，据不完全统计平均每天的客流量约为10万人左右，10万用科学记数法表示为（ ）
| A、1×106 |
| B、10×106 |
| C、1×105 |
| D、10×105 |
如图，已知直线AB∥CD，∠GEB的平分线EF交CD于点F，∠1=42°，则∠2等于（ ）| A、138° | B、142° |
| C、148° | D、159° |
某地为了解气温变化情况，对某月中午12时的气温（单位：℃）进行了统计．如表是根据有关数据制作的统计图表的一部分．
对于四边形ABCD，有4张背面完全相同的纸牌（用①、②、③、④表示），在纸牌的正面分别写有四个不同的条件：①AD=BC；②AB=DC；③AD∥BC；④AB∥DC．小明将这4张纸牌背面朝上洗匀后，先随机摸出一张（不放回），再随机摸出一张．