题目内容
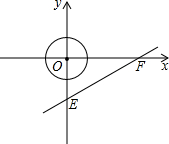 如图所示,在平面直角坐标系中,已知点E和F的坐标分别为E(0,-2)、F(2
如图所示,在平面直角坐标系中,已知点E和F的坐标分别为E(0,-2)、F(2| 3 |
考点:切线的性质,坐标与图形性质
专题:计算题
分析:作OH⊥EF于P,如图,此时点P是直线EF上到圆心O距离最小的点即点P为满足条件的点,连结OA,先利用勾股定理计算出EF=4,再利用面积法计算出OP=
,由于PA、PB为⊙O的切线,根据切线长定理得OP平分∠APB,根据切线的性质得OA⊥PA,则∠APO=
∠APB=30°,然后根据含30度的直角三角形三边的关系在Rt△OPA中可计算出OA.
| 3 |
| 1 |
| 2 |
解答:解:作OH⊥EF于P,如图,此时点P是直线EF上到圆心O距离最小的点,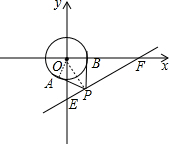
连接OA,
∵E(0,-2)、F(2
,0),
∴OE=2,OF=2
,
∴EF=
=4,
∵
OP•EF=
•OE•OF,
∴OP=
=
,
∵PA、PB为⊙O的切线,
∴OP平分∠APB,OA⊥PA,
∴∠APO=
∠APB=
×60°=30°,
在Rt△OPA中,OA=
OP=
,
即此时⊙O的半径为
.
故答案为

连接OA,
∵E(0,-2)、F(2
| 3 |
∴OE=2,OF=2
| 3 |
∴EF=
| OE2+OF2 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴OP=
2×2
| ||
| 4 |
| 3 |
∵PA、PB为⊙O的切线,
∴OP平分∠APB,OA⊥PA,
∴∠APO=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OPA中,OA=
| 1 |
| 2 |
| ||
| 2 |
即此时⊙O的半径为
| ||
| 2 |
故答案为
| ||
| 2 |
点评:本题考查了圆的切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了切线长定理和坐标与图形性质.

练习册系列答案
相关题目
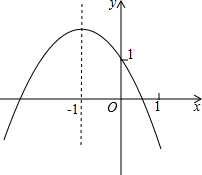 如图为二次函数y=ax2+bx+c(a≠0)的图象,下面四条信息:①4ac<b2<0;②4a+c<2b;③m(am+b)<a-b(m≠-1);④3a+c>0,其中正确信息的个数是( )
如图为二次函数y=ax2+bx+c(a≠0)的图象,下面四条信息:①4ac<b2<0;②4a+c<2b;③m(am+b)<a-b(m≠-1);④3a+c>0,其中正确信息的个数是( ) 如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,点B与点A重合,折痕为DE,求CD的长.
如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,点B与点A重合,折痕为DE,求CD的长.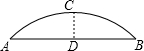 如图,某建筑的屋顶设计成横截面为抛物线形(曲线AOB)的薄壳屋顶,它的拱长AB为4m,拱高CO为0.8m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?
如图,某建筑的屋顶设计成横截面为抛物线形(曲线AOB)的薄壳屋顶,它的拱长AB为4m,拱高CO为0.8m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?