题目内容
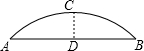 如图,某建筑的屋顶设计成横截面为抛物线形(曲线AOB)的薄壳屋顶,它的拱长AB为4m,拱高CO为0.8m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?
如图,某建筑的屋顶设计成横截面为抛物线形(曲线AOB)的薄壳屋顶,它的拱长AB为4m,拱高CO为0.8m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?考点:二次函数的应用
专题:
分析:首先建立坐标系,进而求出二次函数解析式即可得出模板的轮廓线.
解答: 解:如图所示建立坐标系,
解:如图所示建立坐标系,
则B(4,0),C(2,0.8),
设函数解析式为:y=a(x-2)2+0.8,
将(4,0)代入得出:
0=a(4-2)2+0.8,
解得:a=-0.2,
则抛物线解析式为:y=-0.2(x-2)2+0.8.
 解:如图所示建立坐标系,
解:如图所示建立坐标系,则B(4,0),C(2,0.8),
设函数解析式为:y=a(x-2)2+0.8,
将(4,0)代入得出:
0=a(4-2)2+0.8,
解得:a=-0.2,
则抛物线解析式为:y=-0.2(x-2)2+0.8.
点评:此题主要考查了二次函数的应用,根据题意得出二次函数解析式是解题关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
下列说法中正确的是( )
| A、延长射线OA到点B |
| B、线段AB为直线AB的一部分 |
| C、射线OM与射线MO表示同一条射线 |
| D、一条直线由两条射线组成 |
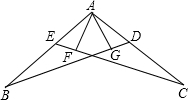 如图,AB=AC,AG⊥BD,AF⊥CE,AG=AF,求证:AD=AE.
如图,AB=AC,AG⊥BD,AF⊥CE,AG=AF,求证:AD=AE. 如图,已知△ABC.
如图,已知△ABC.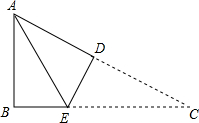 如图,在△ABC中,∠B=90°,∠C=30°,AB=3,BC=3
如图,在△ABC中,∠B=90°,∠C=30°,AB=3,BC=3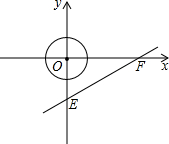 如图所示,在平面直角坐标系中,已知点E和F的坐标分别为E(0,-2)、F(2
如图所示,在平面直角坐标系中,已知点E和F的坐标分别为E(0,-2)、F(2 如图,直线y=x-3分别与x轴、y轴交于点P,F,与双曲线y=
如图,直线y=x-3分别与x轴、y轴交于点P,F,与双曲线y=