题目内容
9.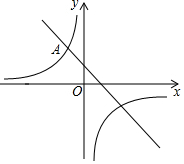 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-x+1的图象的一个交点为A(-1,m).
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-x+1的图象的一个交点为A(-1,m).(1)求这个反比例函数的表达式;
(2)如果一次函数y=-x+1的图象与x轴交于点B(n,0),请确定当x<n时,对应的反比例函数y=$\frac{k}{x}$的值的范围.
分析 (1)由点A在一次函数图象上利用一次函数图象上点的坐标特征即可求出点A的坐标,根据点A的坐标利用反比例函数图象上点的坐标特征即可找出反比例函数表达式;
(2)令一次函数表达式中y=0求出x值,进而可得出点B的坐标,根据点B的横坐标结合图形即可得出结论.
解答 解:(1)∵点A在一次函数y=-x+1的图象上,
∴m=-(-1)+1=2,
∴点A的坐标为(-1,2).
∵点A在反比例函数$y=\frac{k}{x}$的图象上,
∴k=-1×2=-2.
∴反比例函数的表达式为y=-$\frac{2}{x}$.
(2)令y=-x+1=0,解得:x=1,
∴点B的坐标为(1,0),
∴当x=1时,$y=-\frac{2}{x}$=-2.
由图象可知,当x<1时,y>0或y<-2.
点评 本题考查了反比例函数与一次函数的交点问题、一次函数图象上点的坐标特征以及反比例函数图象上点的坐标特征,根据一次函数图象上点的坐标特征求出点A、B的坐标是解题的关键.

练习册系列答案
相关题目
19.下列各式中,计算正确的是( )
| A. | (15x2y-5xy2)÷5xy=3x-5y | B. | 98×102=(100-2)(100+2)=9996 | ||
| C. | $\frac{x}{x+3}-1=\frac{3}{x+3}$ | D. | (3x+1)(x-2)=3x2+x-2 |
20.圆中内接正三角形的边长是半径的( )倍.
| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
17.下列是关于x的一元一次方程的是( )
| A. | x(x-1)=x | B. | x+$\frac{1}{x}$=2 | C. | x=1 | D. | x+2 |
7.把抛物线y=12x2-1先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为( )
| A. | y=12(x+1)2-3 | B. | y=12(x-1)2-3 | C. | y=12(x+1)2+1 | D. | y=12(x-1)2+1 |
 如图,已知△ABC≌△DCB,∠ABC=65°,∠ACB=30°,则∠ACD=35°.
如图,已知△ABC≌△DCB,∠ABC=65°,∠ACB=30°,则∠ACD=35°.