如图.△ABC中.AB=AC.∠BAC=100°.DE垂直平分AB.则∠CAE=60°．题目和参考答案——青夏教育精英家教网—

题目内容

15．

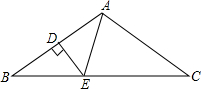如图，△ABC中，AB=AC，∠BAC=100°，DE垂直平分AB，则∠CAE=60°．

分析首先利用三角形的内角和定理和等腰三角形的性质∠B，利用线段垂直平分线的性质易得AE=BE，∠BAE=∠B．

解答解：∵AB=AC，∠BAC=100°，
∴∠B=∠C=（180°-100°）÷2=40°，
∵DE是AB的垂直平分线，
∴AE=BE，
∴∠BAE=∠B=40°，
∴∠CAE=∠BAC-∠BAE=60°，
故答案为：60°．

点评本题主要考查了等腰三角形的性质，三角形的内角和定理，线段垂直平分线的性质，掌握垂直平分线上任意一点，到线段两端点的距离相等和等边对等角是解答此题的关键．

练习册系列答案

相关题目

5．已知4x²-mxy+y²是完全平方式，则m的值是±4．

6．

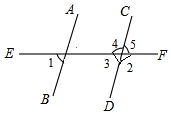如图，已知∠1=80°，则下列结论：①若∠5=80°，则AB∥CD；②若∠2=80°，则AB∥CD；③若∠4=100°，则AB∥CD；④若∠3=100°，则AB∥CD．其中正确的有（　　）

a³•a²=a⁶

x⁵+x⁵=x¹⁰

y⁷•y=y⁸

10．

如图，在平面直角坐标系中，将四边形ABCD先向左平移3个单位，再向上平移2个单位，得到一个新四边形，那么与点A对应的顶点坐标是（　　）

20．科学家发现一种病毒的长度约为0.000036mm，用科学记数法表示这个数为3.6×10^-5mm．

7．阅读情境：
在综合实践课上，同学们探究“全等的等腰直角三角形图形变化问题”，如图1，△ABC≌△ADE，其中，∠B=∠D=90°，AB=BC=AD=DE=2，此时，点C与点E重合．
操作探究1：
（1）小凡将图1中的△ABC沿射线AD方向平移得到△A′B′C′，使点A′在边AD上，线段A′B′与AE相交于点N，线段A′C′与DE相交于点M，请你在图2中画出△ABC平移后某一情形的△A′B′C′，并根据所画图形写出一个正确结论（题目中的已知条件均不能作为结论）；
操作探究2：
（2）小彬将图1中的△ABC绕点A按逆时针方向旋转角度α（0°＜α＜90°），然后，分别延长BC，DE，它们相交于点F，如图3，在操作中，小彬提出如下问题，请你解答：
①当α=30°时，求证：△CEF为等边三角形；
②当α=45°时，四边形ACFE为平行四边形（直接回答即可）；
（3）小颖将图1中的△ABC绕点A按顺时针方向旋转角度β（0°＜β＜90°），线段BC和DE相交于点F，在操作中，小颖提出如下问题，请从下列A、B两个问题中任选一题进行解答．
A：当β=60°时，请在图4中画出旋转得到的图形，并直接写出线段CE的长
B：当旋转到点F是边DE的中点时，请在图4中画出旋转得到的图形，并直接写出线段CE的长．

4．（-$\frac{1}{2}$）^-2-（π-3.14）⁰+（-$\frac{2}{3}$）²⁰¹⁷×（$\frac{3}{2}$）²⁰¹⁷=2．

5．解方程组：
（1）$\left\{\begin{array}{l}{3x+4y=16}\\{5x-6y=33}\end{array}\right.$
（2）$\left\{\begin{array}{l}{2（x-1）-3（y+1）=12}\\{\frac{x}{2}+\frac{y}{3}=1}\end{array}\right.$．

试题分类