题目内容
1.计算:($\frac{2}{{\sqrt{2}+1}}+\frac{2}{{\sqrt{3}+\sqrt{2}}}+\frac{2}{{\sqrt{4}+\sqrt{3}}}+…+\frac{2}{{\sqrt{2002}+\sqrt{2001}}}$)•($\sqrt{2002}$+1)=4002.分析 根据分母有理化可以对原始化简,然后再根据平方差公式进行计算即可解答本题.
解答 解:($\frac{2}{{\sqrt{2}+1}}+\frac{2}{{\sqrt{3}+\sqrt{2}}}+\frac{2}{{\sqrt{4}+\sqrt{3}}}+…+\frac{2}{{\sqrt{2002}+\sqrt{2001}}}$)•($\sqrt{2002}$+1)
=$[2(\sqrt{2}-1)+2(\sqrt{3}-\sqrt{2})+2(\sqrt{4}-\sqrt{3})+…+2(\sqrt{2002}-\sqrt{2001})]•(\sqrt{2002}+1)$
=2[$\sqrt{2}-1+\sqrt{3}-\sqrt{2}+\sqrt{4}-\sqrt{3}+…+\sqrt{2002}-\sqrt{2001}$]$•(\sqrt{2002}+1)$
=2$(\sqrt{2002}-1)(\sqrt{2002}+1)$
=2×(2002-1)
=2×2001
=4002,
故答案为:4002.
点评 本题考查二次根式的混合运算,解题的关键是明确二次根式混合运算的计算方法.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
13.据报道,投资270亿元的西环高铁预计今年底建成通车,通车后能使西环高铁经过的市县约4360000人受益,数据4360000用科学记数法表示为( )
| A. | 436×104 | B. | 4.36×105 | C. | 4.36×106 | D. | 4.36×107 |
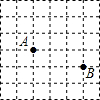 如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都是图中的格点,其中点A、点B的位置如图所示,则点C可能的位置共有( )
如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都是图中的格点,其中点A、点B的位置如图所示,则点C可能的位置共有( )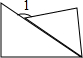 一副三角尺如图所示放置,使三角尺的30°角的顶点重合,且两直角三角尺的斜边重合,直角顶点在斜边的两侧,则∠1的度数是135°.
一副三角尺如图所示放置,使三角尺的30°角的顶点重合,且两直角三角尺的斜边重合,直角顶点在斜边的两侧,则∠1的度数是135°. 如图,直线CD上有一点O,过点O作OA⊥CD,OB平分∠AOD,则∠BOC的度数是135°.
如图,直线CD上有一点O,过点O作OA⊥CD,OB平分∠AOD,则∠BOC的度数是135°.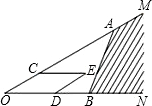 如图,点A、B分别在射线OM、ON上,C、D分别是线段OA和OB上的点,以OC、OD为邻边作平行四边形OCED,下面给出三种作法的条件:
如图,点A、B分别在射线OM、ON上,C、D分别是线段OA和OB上的点,以OC、OD为邻边作平行四边形OCED,下面给出三种作法的条件: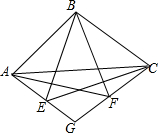 如图,Rt△ABC中,∠ABC=90°,以BA、BC为边向内作等边ABF和等边BCE,AE与CF交于G点,以下结论:①AE=CF;②∠AGC=120°;③GB平分∠AGC;④若AB=BC,则AE=2EG,其中正确的结论有( )
如图,Rt△ABC中,∠ABC=90°,以BA、BC为边向内作等边ABF和等边BCE,AE与CF交于G点,以下结论:①AE=CF;②∠AGC=120°;③GB平分∠AGC;④若AB=BC,则AE=2EG,其中正确的结论有( )