题目内容
15.如图,P为正方形ABCD边CD上任一点,BG⊥AP于G,E为AP上一点,使AG=EG,连接BE、CE(1)求证:BE=BC;
(2)∠CBE的平分线交AE延长于点N,连接DN,求证:BN+DN=$\sqrt{2}$AN.
(3)若正方形边长为2,当P为CD的中点时,直接写出CE长为$\frac{2\sqrt{10}}{5}$.
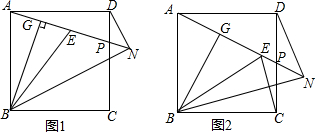
分析 (1)根据线段垂直平分线性质得:AB=BE,又因为正方形ABCD的边长相等,根据等量代换可得结论;
(2)作辅助线,构建两三角形全等,得AG=DH,BG=AH,再证明△BGN和△DHN是等腰直角三角形,得BN=$\sqrt{2}$BG,DN=$\sqrt{2}$HN,相加即可;
(3)连接CN,证明△DHP≌△CNP,根据勾股定理求AP的长,再由面积相等求DH的长,则NC=DH,最后由等腰直角三角形求出CE的长.
解答 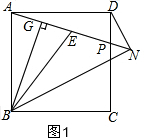 证明:(1)如图1,∵AG=EG,BG⊥AP于G,
证明:(1)如图1,∵AG=EG,BG⊥AP于G,
∴AB=BE,
∵四边形ABCD为正方形,
∴AB=BC,
∴BC=BE;
(2)过D作DH⊥AN于H,
∵AB=AD,∠AGB=∠AHD=90°,∠BAG=∠ADH,
∴△ABG≌△DAH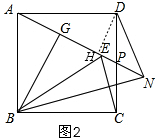 ,
,
∴BG=AH,AG=DH,
∵∠ABG=∠EBG,∠EBN=∠CBN,
∴∠ABG+∠CBN=∠EBG+∠EBN,
∴∠ABC=90°,
∴∠GBN=45°,
∴△BGN是等腰直角三角形,
∴BN=$\sqrt{2}$BG,BG=NG,
∴AH-GH=NG-GH,
∴AG=HN=DH,
∴△DHN也是等腰直角三角形,
∴DN=$\sqrt{2}$HN,
∴AN=AH+HN=BG+HN,
∴$\sqrt{2}$BG+$\sqrt{2}$HN=$\sqrt{2}$AN,
∴BN+DN=$\sqrt{2}$AN;
(3)如图3,连接CN,由勾股定理得:AP=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,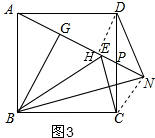
∴S△ADP=$\frac{1}{2}$AD•DP=$\frac{1}{2}$AP•DH,
∴DH=$\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
∵DP=PC,∠DPH=∠CPN,∠DHP=∠PNC=90°,
∴△DHP≌△CNP,
∴CN=DH,
∵BE=BC,BN平分∠EBC,
∴BN⊥EC,
∴CE=$\sqrt{2}$CN=$\sqrt{2}$×$\frac{2\sqrt{5}}{5}$=$\frac{2\sqrt{10}}{5}$.
点评 本题是四边形的综合题,考查了正方形、全等三角形、等腰直角三角形的性质和判定,若题目中出现$\sqrt{2}$倍的关系,首先要考虑应该放在等腰直角三角形中,因为等腰直角三角形的斜边是任一直角边的$\sqrt{2}$倍;因此第二问的和的关系,要把三条线段转化为一条线段,还要放在等腰直角三角形中.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 2a3+3a3=5a6 | B. | (x5)3=x8 | ||
| C. | -2m(m-3)=-2m2-6m | D. | (-3a-2)(-3a+2)=9a2-4 |
 在恩施州2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成如下不完整的统计图表,请根据图表解答下列问题.
在恩施州2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成如下不完整的统计图表,请根据图表解答下列问题.| 获奖等级 | 频数 |
| 一等奖 | 100 |
| 二等奖 | a |
| 三等奖 | 275 |
(2)扇形统计图中表示获得一等奖的扇形的圆心角为72度.
(3)估计全州有多少名学生获得三等奖?

 小明要测量公园被湖水隔开的两棵大树A和B之间的距离,他在A处测得大树B在A的北偏西30°方向,他从A处出发向北偏东15°方向走了200米到达C处,测得大树B在C的北偏西60°方向.
小明要测量公园被湖水隔开的两棵大树A和B之间的距离,他在A处测得大树B在A的北偏西30°方向,他从A处出发向北偏东15°方向走了200米到达C处,测得大树B在C的北偏西60°方向.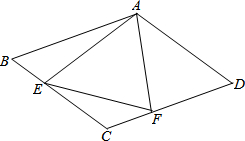 如图所示,在菱形ABCD中,AB=8cm,∠BAD=120°,点E、F分别是边BC、CD上的两个动点,E点从点B向点C运动,F点从点D向点C运动,设点E、F运动的路径长分别是acm和bcm.
如图所示,在菱形ABCD中,AB=8cm,∠BAD=120°,点E、F分别是边BC、CD上的两个动点,E点从点B向点C运动,F点从点D向点C运动,设点E、F运动的路径长分别是acm和bcm. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器,其限制电流不能超过10A,那么用电器可变电阻R应控制的范围是R≥3.6.
已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器,其限制电流不能超过10A,那么用电器可变电阻R应控制的范围是R≥3.6.