题目内容
5.在△ABC中,AB=AC,AD是BC上的高,∠B=30°,AD=1,则△ABC的面积=$\sqrt{3}$.分析 根据直角三角形的性质求出BC的长,根据三角形面积公式求出△ABC的面积.
解答 解:∵DA⊥BC,∠B=30°,
∴AB=2AD=2,
由勾股定理得BD=$\sqrt{3}$,
∵AB=AC,∴BC=2BD=2$\sqrt{3}$,
∴△ABC的面积=$\frac{1}{2}$×BC×AD=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题考查的是直角三角形的性质,掌握在直角三角形中,30°所对的直角边等于斜边的一半是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.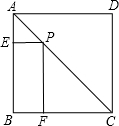 如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于E,PF⊥BC于F,若AC=$\sqrt{2}$,则四边形PEBF的周长为( )
如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于E,PF⊥BC于F,若AC=$\sqrt{2}$,则四边形PEBF的周长为( )
 如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于E,PF⊥BC于F,若AC=$\sqrt{2}$,则四边形PEBF的周长为( )
如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于E,PF⊥BC于F,若AC=$\sqrt{2}$,则四边形PEBF的周长为( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | 1 |
20.在直角三角形中,最大边的长度是最小边长度的2倍,那么最小内角的角度为( )
| A. | 15゜ | B. | 30゜ | C. | 45゜ | D. | 60゜ |
14.下列各组数中,互为倒数的是( )
| A. | -2与-$\frac{1}{2}$ | B. | 0.1与1 | C. | -2与$\frac{1}{2}$ | D. | -43与43 |
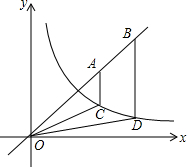 如图,点A,B为直线y=x上的两点,过A,B两点分别作y轴的平行线交双曲线$y=\frac{1}{x}$(x>0)于C,D两点.若BD=2AC.
如图,点A,B为直线y=x上的两点,过A,B两点分别作y轴的平行线交双曲线$y=\frac{1}{x}$(x>0)于C,D两点.若BD=2AC.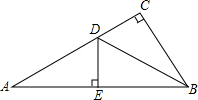 如图,在△ABC中,∠C=90°,∠A=30°,边AB的垂直平分线DE交AC于D,若CD=10cm,则AD=20cm.
如图,在△ABC中,∠C=90°,∠A=30°,边AB的垂直平分线DE交AC于D,若CD=10cm,则AD=20cm.