题目内容
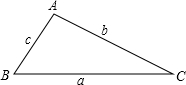
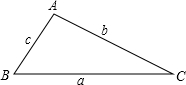
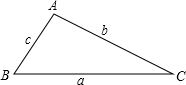
设△ABC的三边分别是a、b、c，其中a b满足于|a+b-4|+（a-b-2）2=0，则第三边c的长的取值范围是：________．
2＜c＜4
分析：先根据非负数的性质求出ab的值，再根据三角形的三边关系求出c的取值范围即可．
解答：∵a b满足于|a+b-4|+（a-b-2）2=0，
∴
，解得
，
∵△ABC的三边分别是a、b、c，
∴3-1＜c＜3+1，即2＜c＜4．
故答案为：2＜c＜4．
点评：本题考查的是三角形的三边关系及非负数的性质，熟知三角形任意两边之和大于第三边是解答此题的关键．
分析：先根据非负数的性质求出ab的值，再根据三角形的三边关系求出c的取值范围即可．
解答：∵a b满足于|a+b-4|+（a-b-2）2=0，
∴
，解得，∵△ABC的三边分别是a、b、c，
∴3-1＜c＜3+1，即2＜c＜4．
故答案为：2＜c＜4．
点评：本题考查的是三角形的三边关系及非负数的性质，熟知三角形任意两边之和大于第三边是解答此题的关键．
练习册系列答案
相关题目
（a+b+c）
