Question

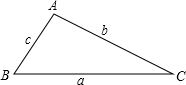
①设△ABC的三边分别为a、b、c，试证明：a＜

1

2

（a+b+c）

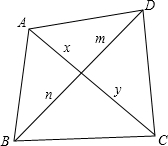
②设四边形的四边长依次为a、b、c、d，两条对角线分别为e、f，证明：e+f＞

1

2

（a+b+c+d）

Answer 1

分析：①根据三角形三边关系可知b+c＞a，再根据不等式的性质b+c+a＞a+a，即可证明a＜

1

2

（a+b+c）；
②根据三角形三边关系可得n+x＞a，x+m＞b，y+m＞c，n+y＞d，再根据不等式的性质可得2（x+y+m+n）＞a+b+c+d，从而证明e+f＞

1

2

（a+b+c+d）．

解答：解：①证明：∵b+c＞a，
∴

1

2

b+

1

2

c＞

1

2

a，
∴

1

2

b+

1

2

c+

1

2

a＞

1

2

a+

1

2

a，
∴

1

2

（a+b+c）＞a，即a＜

1

2

（a+b+c）；

②证明：显然n+x＞a，x+m＞b，y+m＞c，n+y＞d，
所以：2（x+y+m+n）＞a+b+c+d，
即：2（e+f）＞a+b+c+d，
所以：e+f＞

1

2

（a+b+c+d）．

点评：本题综合考查了三角形三边关系和不等式的性质，三角形三边关系定理：三角形任意两边之和大于第三边．