题目内容
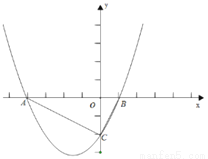
如图,已知抛物线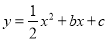 轴交于点A(-4,0)和B(1,0)两点,与y轴交于C点.
轴交于点A(-4,0)和B(1,0)两点,与y轴交于C点.
(1)求此抛物线的解析式;
(2)设E是线段AB上的动点,作EF∥AC交BC于F,连接CE,当△CEF的面积是△BEF面积的2倍时,求E点的坐标;
(3)若P为抛物线上A、C两点间的一个动点,过P作y轴的平行线,交AC于Q,当P点运动到什么位置时,线段PQ的值最大,并求此时P点的坐标.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
如图,已知抛物线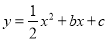 轴交于点A(-4,0)和B(1,0)两点,与y轴交于C点.
轴交于点A(-4,0)和B(1,0)两点,与y轴交于C点.
(1)求此抛物线的解析式;
(2)设E是线段AB上的动点,作EF∥AC交BC于F,连接CE,当△CEF的面积是△BEF面积的2倍时,求E点的坐标;
(3)若P为抛物线上A、C两点间的一个动点,过P作y轴的平行线,交AC于Q,当P点运动到什么位置时,线段PQ的值最大,并求此时P点的坐标.

 名校课堂系列答案
名校课堂系列答案