Question

18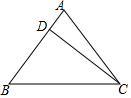．如图，等腰△ABC的底边BC=20cm，D是AB边上的一点，CD=16cm，BD=12cm，求△ABC的面积．

Answer 1

分析 先利用勾股定理逆定理判断出△BCD是直角三角形，然后设AC=AB=x，表示出AD，在Rt△ACD中，利用勾股定理列出方程求解即可得到AC，利用AB和AB边上的高列式计算即可得解．

解答 解：∵BD²+CD²=12²+16²=400，
BC²=20²=400，
∴BD²+CD²=BC²，
∴△BCD是直角三角形，∠BDC=90°，
设AC=AB=x，
∵BD=12cm，
∴AD=x-12，
在Rt△ACD中，AD²+CD²=AC²，
即（x-12）²+16²=x²，
解得x=$\frac{50}{3}$，
即AC=AB=$\frac{50}{3}$cm，
∴△ABC的面积=$\frac{1}{2}$×AB•CD=$\frac{1}{2}$×$\frac{50}{3}$×16=$\frac{400}{3}$cm²．

点评 本题考查了勾股定理逆定理，勾股定理的应用，熟记两个定理并判断出△BCD是直角三角形，然后求出AB的长是解题的关键．