题目内容
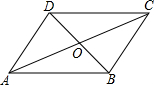 求证:在平行四边形ABCD中,AC2+BD2=AB2+BC2+CD2+DA2.
求证:在平行四边形ABCD中,AC2+BD2=AB2+BC2+CD2+DA2.考点:平行四边形的性质,勾股定理
专题:证明题
分析:作DE⊥BA于点E,CF⊥AB交AB的延长线于F,再根据四边形ABCD是平行四边形,求证△ADE≌△BCF,得出DE=CF,AE=BF,由勾股定理得AC2=AF2+CF2=CF2+(AB+AE)2,BD2=DE2+BE2=CF2+(AB-AE)2,AD2=AE2+DE2,CB2=BF2+CF2,所以AC2+BD2=AB2+BC2+CD2+DA2.
解答: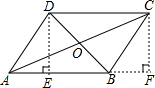 证明:作DE⊥BA于点E,CF⊥AB交AB的延长线于F,则∠AED=∠BFC=90°.
证明:作DE⊥BA于点E,CF⊥AB交AB的延长线于F,则∠AED=∠BFC=90°.
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥CD,
∴∠DAE=∠CBF,
在△ADE和△BCF中,
,
∴△ADE≌△BCF(AAS),
∴AE=BF,DE=CF.
在Rt△DBE和Rt△CAF中,由勾股定理,得
AC2=AF2+CF2=CF2+(AB+AE)2,
BD2=DE2+BE2=CF2+(AB-AE)2,
AD2=AE2+DE2,CB2=BF2+CF2,
则AC2+BD2=CF2+AB2+AE2+2AB•AE+CF2+AB2-2AB•AE+AE2
=(CF2+AE2)+(CF2+AE2)+AB2+AB2
=AB2+BC2+CD2+DA2.
故AC2+BD2=AB2+BC2+CD2+DA2.
 证明:作DE⊥BA于点E,CF⊥AB交AB的延长线于F,则∠AED=∠BFC=90°.
证明:作DE⊥BA于点E,CF⊥AB交AB的延长线于F,则∠AED=∠BFC=90°.∵四边形ABCD是平行四边形,
∴AB=DC,AB∥CD,
∴∠DAE=∠CBF,
在△ADE和△BCF中,
|
∴△ADE≌△BCF(AAS),
∴AE=BF,DE=CF.
在Rt△DBE和Rt△CAF中,由勾股定理,得
AC2=AF2+CF2=CF2+(AB+AE)2,
BD2=DE2+BE2=CF2+(AB-AE)2,
AD2=AE2+DE2,CB2=BF2+CF2,
则AC2+BD2=CF2+AB2+AE2+2AB•AE+CF2+AB2-2AB•AE+AE2
=(CF2+AE2)+(CF2+AE2)+AB2+AB2
=AB2+BC2+CD2+DA2.
故AC2+BD2=AB2+BC2+CD2+DA2.
点评:此题主要考查学生对勾股定理、平行四边形的性质和全等三角形的性质的理解和掌握,此题涉及到的知识点较多,综合性很强,有一定的拔高难度,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

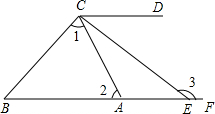 如图,∠B=42°,∠1=∠2+10°,∠ACD=64°,∠ACD的平分线与BA的延长线相交于点E.
如图,∠B=42°,∠1=∠2+10°,∠ACD=64°,∠ACD的平分线与BA的延长线相交于点E. 如图,AB∥CD,OF平分∠AOE,∠1=40°,则∠2是多少度?
如图,AB∥CD,OF平分∠AOE,∠1=40°,则∠2是多少度? 如图,在直角坐标系中,如果△AOB≌△COD,并且A,D两点的坐标分别为A(0,3)和D(0,-2),那么B点坐标
如图,在直角坐标系中,如果△AOB≌△COD,并且A,D两点的坐标分别为A(0,3)和D(0,-2),那么B点坐标