题目内容
11. 如图:在△ABC中,点D,E在BC上,且AD=AE,BD=CE,∠ADE=∠AED,求证:AB=AC.
如图:在△ABC中,点D,E在BC上,且AD=AE,BD=CE,∠ADE=∠AED,求证:AB=AC.
分析 由∠ADE=∠AED,得∠ADB=∠AEC,再根据SAS证明△ABD≌△ACE,即可得出AB=AC.
解答 证明:∵∠ADE=∠AED,
∴∠ADB=∠AEC,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AD=AE}\\{∠ADB=∠AEC}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△ACE(SAS),
∴AB=AC.
点评 本题考查了全等三角形的判定和性质,找出已知边的夹角相等是证明三角形全等的关键,也是本题的突破点.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
2. 如图,直线AB∥CD,直线EF与AB,CD相交于点E,F,∠BEF的平分线与CD相交于点N.若∠1=63°,则∠2=( )
如图,直线AB∥CD,直线EF与AB,CD相交于点E,F,∠BEF的平分线与CD相交于点N.若∠1=63°,则∠2=( )
 如图,直线AB∥CD,直线EF与AB,CD相交于点E,F,∠BEF的平分线与CD相交于点N.若∠1=63°,则∠2=( )
如图,直线AB∥CD,直线EF与AB,CD相交于点E,F,∠BEF的平分线与CD相交于点N.若∠1=63°,则∠2=( )| A. | 64° | B. | 63° | C. | 60° | D. | 54° |
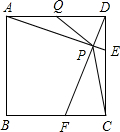 在边长为2cm的正方形ABCD中,动点E、F分别从D、C两点同时出发,都以1cm/s的速度在射线DC、CB上移动.连接AE和DF交于点P,点Q为AD的中点.若以A、P、Q为顶点的三角形与以P、D、C为顶点的三角形相似,则运动时间t为2或4秒.
在边长为2cm的正方形ABCD中,动点E、F分别从D、C两点同时出发,都以1cm/s的速度在射线DC、CB上移动.连接AE和DF交于点P,点Q为AD的中点.若以A、P、Q为顶点的三角形与以P、D、C为顶点的三角形相似,则运动时间t为2或4秒.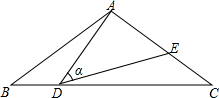 如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$,则线段CE的最大值为6.4.
如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$,则线段CE的最大值为6.4.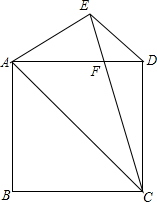 如图,正方形ABCD中,过D作DE∥AC,∠ACE=30°,CE交AD于点F,求证:AC=EC.
如图,正方形ABCD中,过D作DE∥AC,∠ACE=30°,CE交AD于点F,求证:AC=EC. 拱桥截面是一条抛物线,如图所示,现测得水面宽AB=16m,拱顶O到水面的距离为8m,在图中的直角坐标系内,拱桥所在抛物线的解析式是y=-$\frac{1}{8}$x2.
拱桥截面是一条抛物线,如图所示,现测得水面宽AB=16m,拱顶O到水面的距离为8m,在图中的直角坐标系内,拱桥所在抛物线的解析式是y=-$\frac{1}{8}$x2.