题目内容
11.解方程组:①$\left\{\begin{array}{l}{x+y=4}\\{2x-y=-1}\end{array}\right.$
②$\left\{\begin{array}{l}{4x-3y=11}\\{2x+y=13}\end{array}\right.$.
分析 ①方程组利用加减消元法求出解即可;
②方程组利用加减消元法求出解即可.
解答 解:①$\left\{\begin{array}{l}{x+y=4①}\\{2x-y=-1②}\end{array}\right.$,
①+②得:3x=3,即x=1,
把x=1代入①得:y=3,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$;
②$\left\{\begin{array}{l}{4x-3y=11①}\\{2x+y=13②}\end{array}\right.$,
②×2-①得:5y=15,即y=3,
①+②×3得:10x=50,即x=5,
则方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=3}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
2. 如图,∠B=∠C,增加哪个条件可以让△ABD≌△ACE?( )
如图,∠B=∠C,增加哪个条件可以让△ABD≌△ACE?( )
 如图,∠B=∠C,增加哪个条件可以让△ABD≌△ACE?( )
如图,∠B=∠C,增加哪个条件可以让△ABD≌△ACE?( )| A. | BD=AD | B. | AB=AC | C. | ∠1=∠2 | D. | 以上答案都不对 |
19.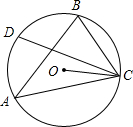 如图,点O为锐角△ABC的外心,点D为劣弧AB的中点,若∠BAC=α,∠ABC=β,且β>α,则∠DCO=( )
如图,点O为锐角△ABC的外心,点D为劣弧AB的中点,若∠BAC=α,∠ABC=β,且β>α,则∠DCO=( )
 如图,点O为锐角△ABC的外心,点D为劣弧AB的中点,若∠BAC=α,∠ABC=β,且β>α,则∠DCO=( )
如图,点O为锐角△ABC的外心,点D为劣弧AB的中点,若∠BAC=α,∠ABC=β,且β>α,则∠DCO=( )| A. | $\frac{β-α}{2}$ | B. | $\frac{α-β}{3}$ | C. | $\frac{β+α}{3}$ | D. | $\frac{β+α}{4}$ |
3. 已知有理数a、b在数轴上的位置如图所示,下列结论正确的是( )
已知有理数a、b在数轴上的位置如图所示,下列结论正确的是( )
 已知有理数a、b在数轴上的位置如图所示,下列结论正确的是( )
已知有理数a、b在数轴上的位置如图所示,下列结论正确的是( )| A. | a>b | B. | ab<0 | C. | b-a>0 | D. | a+b>0 |
20. 已知a、b、c在数轴上的位置如图所示,则下列说法正确的是( )
已知a、b、c在数轴上的位置如图所示,则下列说法正确的是( )
 已知a、b、c在数轴上的位置如图所示,则下列说法正确的是( )
已知a、b、c在数轴上的位置如图所示,则下列说法正确的是( )| A. | a<0 | B. | b<c | C. | b>a | D. | c>0 |
1.已知点P(a,a+3)在抛物线y=x2-7x+19图象上,则点P关于原点O的对称点P′的坐标是( )
| A. | (4,7) | B. | (-4,-7) | C. | (4,-7) | D. | (-4,7) |
 如图是7×7的网格,每个顶点叫格点,请在图中画一个面积为20的正方形,并求这个正方形的边长.
如图是7×7的网格,每个顶点叫格点,请在图中画一个面积为20的正方形,并求这个正方形的边长. 如图,已知:AC、BD相交于E,DE=CE,∠BAC=∠ABD,则图中有2个等腰三角形,3对全等三角形.
如图,已知:AC、BD相交于E,DE=CE,∠BAC=∠ABD,则图中有2个等腰三角形,3对全等三角形.