题目内容
 如图,矩形ABCD的对角线AC,BD交于点O,DE∥AC交BA的延长线于点E,点F在BC上,BF=BO,且AE=6,AD=8.
如图,矩形ABCD的对角线AC,BD交于点O,DE∥AC交BA的延长线于点E,点F在BC上,BF=BO,且AE=6,AD=8.(1)求BF的长;
(2)求四边形OFCD的面积.
考点:矩形的性质,勾股定理,三角形中位线定理,平行四边形的判定与性质
专题:
分析:(1)在Rt△EAD中,利用勾股定理求得DE=10;然后利用?ACDE的对边相等得到:AC=DE=10;最后在Rt△ABC中根据“直角三角形斜边上的中线等于斜边的一半”和已知条件来求BF=BO=5;
(2)过点O作OG⊥BC于点G.由图形得到S四边形OFCD=S△BCD-S△BOF=
.利用三角形中位线定理得到OG是△BCD的中位线.利用(1)中平行四边形ACDE的性质求得相关线段的长度,将其代入进行计算即可.
(2)过点O作OG⊥BC于点G.由图形得到S四边形OFCD=S△BCD-S△BOF=
| 33 |
| 2 |
解答: 解:(1)∵四边形ABCD是矩形,
解:(1)∵四边形ABCD是矩形,
∴∠BAD=90°,
∴∠EAD=180°-∠BAD=90°.
∵在Rt△EAD中,AE=6,AD=8,
∴DE=
=10.
∵DE∥AC,AB∥CD,
∴四边形ACDE是平行四边形.
∴AC=DE=10.
在Rt△ABC中,∠ABC=90°,
∵OA=OC,
∴BO=
AC=5.
∵BF=BO,
∴BF=5.
(2)过点O作OG⊥BC于点G.
∵四边形ABCD是矩形,
∴∠BCD=90°,
∴CD⊥BC.
∴OG∥CD.
∵OB=OD,∴BG=CG,
∴OG是△BCD的中位线.
由(1)知,四边形ACDE是平行四边形,AE=6,
∴CD=AE=6.
∴OG=
CD=3.
∵AD=8,
∴BC=AD=8.
∴S△BCD=
•BC•CD=24,S△BOF=
•BF•OG=
.
∴S四边形OFCD=S△BCD-S△BOF=
.
其他证法相应给分.
 解:(1)∵四边形ABCD是矩形,
解:(1)∵四边形ABCD是矩形,∴∠BAD=90°,
∴∠EAD=180°-∠BAD=90°.
∵在Rt△EAD中,AE=6,AD=8,
∴DE=
| AE2+AD2 |
∵DE∥AC,AB∥CD,
∴四边形ACDE是平行四边形.
∴AC=DE=10.
在Rt△ABC中,∠ABC=90°,
∵OA=OC,
∴BO=
| 1 |
| 2 |
∵BF=BO,
∴BF=5.
(2)过点O作OG⊥BC于点G.
∵四边形ABCD是矩形,
∴∠BCD=90°,
∴CD⊥BC.
∴OG∥CD.
∵OB=OD,∴BG=CG,
∴OG是△BCD的中位线.
由(1)知,四边形ACDE是平行四边形,AE=6,
∴CD=AE=6.
∴OG=
| 1 |
| 2 |
∵AD=8,
∴BC=AD=8.
∴S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
∴S四边形OFCD=S△BCD-S△BOF=
| 33 |
| 2 |
其他证法相应给分.
点评:本题综合考查了三角形中位线定理,矩形的性质,平行四边形的判定与性质以及勾股定理等知识.解题时,要注意数形结合.

练习册系列答案
相关题目
点P(x,y)以方程组
的解为单位,则点P在( )
|
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
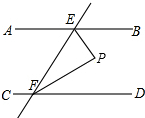 请将下列证明过程补充完整:
请将下列证明过程补充完整: 已知:如图,?ABCD中,E,F两点在对角线BD上,BE=DF.
已知:如图,?ABCD中,E,F两点在对角线BD上,BE=DF.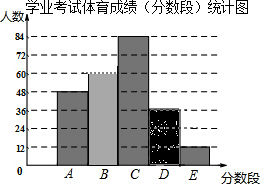 为了了解我市初四学生学业考试体育成绩,现从全市该年级学生中随机抽取了240名学生的体育成绩进行统计分段(A:100~90分;B:90~80分;C:80~70分;D:70~60分;E:60分以下)后,作出了频数分布直方图的一部分(每组数据含最大值,不含最小值).请根据频数分布直方图,解答下列问题:
为了了解我市初四学生学业考试体育成绩,现从全市该年级学生中随机抽取了240名学生的体育成绩进行统计分段(A:100~90分;B:90~80分;C:80~70分;D:70~60分;E:60分以下)后,作出了频数分布直方图的一部分(每组数据含最大值,不含最小值).请根据频数分布直方图,解答下列问题: