题目内容
若一个三角形三个内角度数的比为1：2：3，那么这个三角形最小角的正切值为 ．
考点：特殊角的三角函数值
专题：
分析：设这三个内角分别为x，2x，3x，根据三角形的内角和为180°，列方程求出角的度数，然后根据特殊角的三角函数值求出最小角的正切值．
解答：解：设这三个内角分别为x，2x，3x，
由题意得，x+2x+3x=180°，
解得：x=30°，
即最小角为30°，
则tan30°=
．
故答案为：
．
由题意得，x+2x+3x=180°，
解得：x=30°，
即最小角为30°，
则tan30°=
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题考查了特殊角的三角函数值，解答本题的关键是根据三角形的内角和公式求出角的度数．
练习册系列答案
新思维寒假作业系列答案
相关题目
如图的正方形网格中，每个小正方形边长均为1，点A固定在格点（即小正方形的顶点）上，请按步骤要求作图并解答：
如图，平行四边形ABCD的顶点O，A，C的坐标分别是（0，0），（a，0），
如图，EG、AF、CB三条直线两两相交，AB、DE分别是∠GAD、∠FDC的角平分线，若AB=AD=DE，则∠DAC=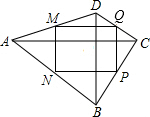
如图，在四边形ABCD中，M、N、P、Q分别是AD、AB、BC、CD的中点，且对角线AC⊥BD，AC：BD=4：3，AC+BD=28，则MQ：QP=