题目内容
|x+
|+|2x+4
|的最小值的整数部分是
.
| 2 |
| 3 |
考点:二次根式的混合运算,绝对值,估算无理数的大小
专题:计算题
分析:令x+
=0,2x+4
=0,解得x=-
,x=-2
,根据这两个值将数轴分成三部分,对原式化简,再求其最小值,得到最小值的整数部分.
| 2 |
| 3 |
| 2 |
| 3 |
解答:解:当x≤-2
时,原式=-x-
-2x-4
=-3x-
-4
,
当-2
<x≤-
时,原式=-x-
+2x+4
=x-
+4
,
当x>-
时,原式=x+
+2x+4
=3x+
+4
,
∴当x=-2
时,原式=2
-
,
当x=-
时,原式=4
-2
=2(2
-
)
∴原式最小值为2
-
,其整数部分为2.
故答案为:2.
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
当-2
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
当x>-
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
∴当x=-2
| 3 |
| 3 |
| 2 |
当x=-
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴原式最小值为2
| 3 |
| 2 |
故答案为:2.
点评:本题考查了二次根式的混合运算,绝对值的化简.关键是根据取两个绝对值的“0值点”,分别化简.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
某种商品的市场零售价,去年比前年上涨了25%.有关部门通过宏观调控,稳定了涨幅,使得今年比前年只上涨了15%,则今年比去年的市场零售价降低了( )
| A、8% | B、10% |
| C、11% | D、12% |
已知,如图,⊙O直径AB延长线上一点P,割线PCD交⊙O于C,D. 弦DF⊥AB于H,CF交AB于E,DE⊥CF,∠P=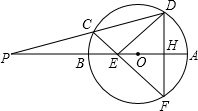 15°,⊙O的半径为2,则CF的大小为( )
15°,⊙O的半径为2,则CF的大小为( )
 15°,⊙O的半径为2,则CF的大小为( )
15°,⊙O的半径为2,则CF的大小为( )A、2
| ||||
B、
| ||||
C、1+
| ||||
D、
|
 如图所示,在△ABC中,DE∥AB∥FG,且FG到DE、AB的距离之比为1:2.若△ABC的面积为32,△CDE的面积为2,则△CFG的面积S等于
如图所示,在△ABC中,DE∥AB∥FG,且FG到DE、AB的距离之比为1:2.若△ABC的面积为32,△CDE的面积为2,则△CFG的面积S等于