题目内容
5．若分式$\frac{1}{x-3}$有意义，则x的取值范围是（ ）| A． | A、x≠3 | B． | x≥3 | C． | x＞3 | D． | x＜3 |
分析 根据分母不等于0列不等式求解即可．
解答 解：由题意得，x-3≠0，
解得x≠3．
故选A．
点评 本题考查了分式有意义的条件，从以下三个方面透彻理解分式的概念：（1）分式无意义?分母为零；（2）分式有意义?分母不为零；（3）分式值为零?分子为零且分母不为零．
练习册系列答案
中考解读考点精练系列答案
相关题目
15．
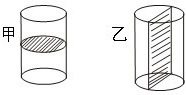图是甲、乙两位同学对同一个圆柱的两种不同的切分方法（平均分成两块），这个圆柱的底面半径为1cm，高为4cm．甲切分后表面积增加了6.28cm2，乙切分后表面积增加了16cm2 （π≈3.14）．
图是甲、乙两位同学对同一个圆柱的两种不同的切分方法（平均分成两块），这个圆柱的底面半径为1cm，高为4cm．甲切分后表面积增加了6.28cm2，乙切分后表面积增加了16cm2 （π≈3.14）． 
17．一元一次方程-2x=4的解是（ ）
| A． | x=-2 | B． | x=2 | C． | x=1 | D． | x=-$\frac{1}{2}$ |
14．某种商品因换季准备打折出售，如果按照原定价的七五折出售，每件将赔10元，而按原定价的九折出售，每件将赚38元，则这种商品的原定价是（ ）
| A． | 200元 | B． | 240元 | C． | 320元 | D． | 360元 |
15．
某鲜花销售部在春节前20天内销售一批鲜花．其中，该销售部公司的鲜花批发部日销售量y1（万朵）与时间x（x为整数，单位：天）关系为二次函数，部分对应值如表所示．
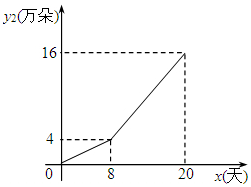
与此同时，该销售部还通过某网络电子商务平台销售鲜花，网上销售日销售量y2（万朵）与时间x（x为整数，单位：天） 的函数关系如图所示．
（1）求y1与x的二次函数关系式及自变量x的取值范围；
（2）求y2与x的函数关系式及自变量x的取值范围；
（3）当8≤x≤20时，设该花木公司鲜花日销售总量为y万朵，写出y与时间x的函数关系式，并判断第几天日销售总量y最大，并求出此时的最大值．
某鲜花销售部在春节前20天内销售一批鲜花．其中，该销售部公司的鲜花批发部日销售量y1（万朵）与时间x（x为整数，单位：天）关系为二次函数，部分对应值如表所示．| 时间x（天） | 0 | 4 | 8 | 12 | 16 | 20 |
| 销量y1（万朵） | 0 | 16 | 24 | 24 | 16 | 0 |
（1）求y1与x的二次函数关系式及自变量x的取值范围；
（2）求y2与x的函数关系式及自变量x的取值范围；
（3）当8≤x≤20时，设该花木公司鲜花日销售总量为y万朵，写出y与时间x的函数关系式，并判断第几天日销售总量y最大，并求出此时的最大值．