题目内容
17.已知二次函数y=2x2+x-3.(1)该函数图象与x轴有几个交点?并求出交点坐标;
(2)试说明一元二次方程2x2+x-3=7的根与二次函数y=2x2+x-3的关系;
(3)当x为何值时,函数y的值为25?
分析 (1)令y=0,求出△,解方程即可;
(2)一元二次方程2x2+x-3=7的根就是当y=7时二次函数y=2x2+x-3中x的对应值;
(3)令y=25,解方程即可.
解答 解:(1)令y=0,则2x2+x-3=0,
∵△=25>0,
∴函数图象与x轴有2个交点,
∵2x2+x-3=0的解为x1=$\frac{3}{2}$,x2=1,
∴函数图象与x轴交点坐标分别为($\frac{3}{2}$,0)(1,0);
(2)一元二次方程2x2+x-3=7的根就是二次函数y=2x2+x-3中当y=7时x的对应值;
(3)令y=25,则2x2+x-3=25,
解得:x1=-4,x2=$\frac{7}{2}$,
∴当x=-4或x=$\frac{7}{2}$时,函数的值为25.
点评 本题主要考查了二次函数与一元二次方程的关系,正确理解二次函数与一元二次方程的关系是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
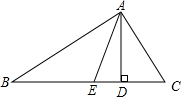 如图,在△ABC中,∠B=40°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线.
如图,在△ABC中,∠B=40°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线.
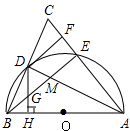 如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E,连接AD、
如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E,连接AD、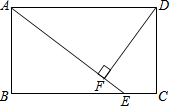 在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.
在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.