题目内容
2.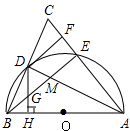 如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E,连接AD、
如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E,连接AD、BE交于点M,过点D作DF⊥AC于点F,DH⊥AB于点H交BE于点G,下列结论:①BD=CD,②DF是⊙O的切线,③∠DAC=∠BDH,④DG=$\frac{1}{2}$BM,其中正确的结论的序号是①②③④.
分析 ①利用直径所对的圆周角是直角,以及等腰三角形的三线合一性质即可得出结论;
②根据垂径定理可以证得OD⊥BE,然后证明DF∥BE,即可证得DF⊥OD,则依据切线的判定定理可以证得;
③利用DH是直角三角形的斜边上的高线,则∠DAB=∠BDH,结合∠BAD=∠DAC即可证得;
④根据等角对等边,可以证得DG=BG,DG=GM即可求证.
解答 解:①∵AB为⊙O的直径,
∴∠BDA=90°,即AD⊥BC,
又∵AB=AC,
∴BD=DC,∠BAD=∠DAE,
故①正确;
②连接OD,如图所示: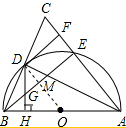
∵∠BAD=∠DAE,
∴$\widehat{BD}=\widehat{DE}$,
∴OD⊥BE,
∵AB是直径,
∴BE⊥AC
又∵DF⊥AC,
∴BE∥DF,
∴DF⊥OD,
∴DF是切线.故②正确;
③∵Rt△ABD中,DH⊥AB,
∴∠DAB=∠BDH,
又∵∠BAD=∠DAC,
∴∠DAC=∠BDH.
故③正确;
④∵∠DBE=∠DAC(同弧所对的圆周角相等),
∠BDH=∠DAC(已证),
∴∠DBE=∠BDH
∴DG=BG,
∵∠BDH+∠HDA=∠DBE+∠DMB=90°,
∴∠GDM=∠DMG
∴DG=GM
∴DG=$\frac{1}{2}$BM,
故④正确.
故答案为:①②③④.
点评 本题考查了切线的性质、三线合一定理、圆周角定理、垂径定理;熟练掌握等腰三角形的性质和圆周角定理,并能进行推理论证是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列说法中正确的是( )
| A. | 已知a,b,c是三角形的三边,则a2+b2=c2 | |
| B. | 在直角三角形中两边和的平方等于第三边的平方 | |
| C. | 在Rt△ABC中,∠C=90°,所以BC2+AC2=AB2 | |
| D. | 在Rt△ABC中,∠B=90°,所以BC2+AC2=AB2 |
7.下列运算正确的是( )
| A. | a2•a3=a6 | B. | a6÷a5=a | C. | (-a2)4=a6 | D. | a2+a3=a5 |
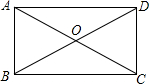 在矩形ABCD中,AC与BD交于点O,∠BOC=120°,AD=6cm,求AC的长.
在矩形ABCD中,AC与BD交于点O,∠BOC=120°,AD=6cm,求AC的长.