题目内容
11.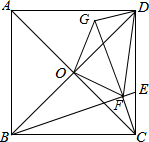 如图,正方形ABCD的边长为12,点O为对角线AC、BD的交点,点E在CD上,tan∠CBE=$\frac{1}{3}$,过点C作CF⊥BE,垂足为F,连接OF,将△OCF绕着点O逆时针旋转90°得到△ODG,连接FG、FD,则△DFG的面积是$\frac{72}{5}$.
如图,正方形ABCD的边长为12,点O为对角线AC、BD的交点,点E在CD上,tan∠CBE=$\frac{1}{3}$,过点C作CF⊥BE,垂足为F,连接OF,将△OCF绕着点O逆时针旋转90°得到△ODG,连接FG、FD,则△DFG的面积是$\frac{72}{5}$.
分析 首先在图1中,证明射影定理AC2=AD•AB,在图2中,根据射影定理证明△BOF∽△BED,得$\frac{OF}{DE}$=$\frac{OB}{BE}$,先求出CF,OF,再求出GD,DG即可解决问题.
解答 解:如图1, ∵CD⊥AB,
∵CD⊥AB,
∴∠ADC=90°,
而∠CAD=∠BAC,
∴Rt△ACD∽Rt△ABC,
∴AC:AB=AD:AC,
∴AC2=AD•AB;
如图2中,∵四边形ABCD为正方形,
∴OC⊥BO,∠BCD=90°,
∴BC2=BO•BD,
∵CF⊥BE,
∴BC2=BF•BE,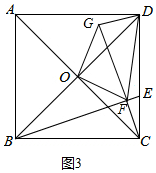
∴BO•BD=BF•BE,
即$\frac{BO}{BE}$=$\frac{BF}{BD}$,
而∠OBF=∠EBD,
∴△BOF∽△BED,
∴$\frac{OF}{DE}$=$\frac{OB}{BE}$,
∵tan∠CBE=$\frac{1}{3}$=$\frac{EC}{BC}$,BC=12,
∴EC=4,BE=$\sqrt{B{C}^{2}+E{C}^{2}}$=4$\sqrt{10}$,DE=8,
∵$\frac{1}{2}$×BC×CE=$\frac{1}{2}$×BE×CF,
∴CF=$\frac{12×4}{4\sqrt{10}}$=$\frac{6\sqrt{10}}{5}$,
∴$\frac{OF}{8}$=$\frac{6\sqrt{2}}{4\sqrt{10}}$,
∴OF=$\frac{12\sqrt{5}}{5}$,
如图3中,∵∠FOC=∠GOD,DG=CF=$\frac{6\sqrt{10}}{5}$,
∴∠GOF=∠DOC=90°,
∵OF=OG,
∴∠OFG=∠OGF=45°,
∴FG=$\sqrt{2}$OF=$\frac{12\sqrt{10}}{5}$,∠OFG=∠OGD=135°,
∴∠DGF=∠OGD-∠OGF=90°,
∴S△DGF=$\frac{1}{2}$×DG×GF=$\frac{1}{2}$×$\frac{6\sqrt{10}}{5}$×$\frac{12\sqrt{10}}{5}$=$\frac{72}{5}$.
故答案为$\frac{72}{5}$.
点评 本题考查正方形的性质、直角三角形的性质、旋转变换、射影定理、相似三角形的判定和性质等知识,解题的关键是利用射影定理证明两个三角形相似,题目比较难,属于中考填空题中的压轴题.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案| A. | -12-8-3+4 | B. | -12-8+3+4 | C. | -12+8+3+4 | D. | 12-8-3-4 |
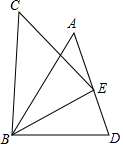 如图,已知,△ABD≌△CBE,下列结论不正确的是( )
如图,已知,△ABD≌△CBE,下列结论不正确的是( )| A. | ∠CBE=∠ABD | B. | BE=BD | C. | ∠CEB=∠BDE | D. | AE=ED |
| A. | 12-8-7+15 | B. | -12+18+7-15 | C. | 12+18+7-15 | D. | 12+18-7-15 |
| A. | 小于8 | B. | 等于8 | C. | 等于4 | D. | 小于4 |
 如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=8,则图中阴影部分的面积是( )
如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=8,则图中阴影部分的面积是( )| A. | 8π | B. | 4π | C. | 64π | D. | 16π |
| A. | 6a-5a=1 | B. | a3•a3=a9 | C. | a6÷a3=a2 | D. | (a2)3=a6 |
| A. | 3x2-6xy+2=0 | B. | x2-5=-2x | C. | x2+3x-1=x2 | D. | x2+$\frac{1}{x}$=0 |