题目内容
3. 如图,在四边形ABCD中,AD∥BC,∠B=60°,E为AB的中点,EC⊥AB,若AD=2,AB=6.则CD的长度为2$\sqrt{7}$.
如图,在四边形ABCD中,AD∥BC,∠B=60°,E为AB的中点,EC⊥AB,若AD=2,AB=6.则CD的长度为2$\sqrt{7}$.
分析 过A点作AF⊥BC于F,过D点作DG⊥BC于G,则四边形AFGD是矩形,在Rt△AFB中,根据含30度角的直角三角形的性质可得BF=3,根据勾股定理可得AF=3$\sqrt{3}$,根据矩形的性质可得DG=3$\sqrt{3}$,FG=2,进一步得到CG=BC-BF-FG=1,再在Rt△CGD中,根据勾股定理可得CD=2$\sqrt{7}$.
解答  解:过A点作AF⊥BC于F,过D点作DG⊥BC于G,则四边形AFGD是矩形,
解:过A点作AF⊥BC于F,过D点作DG⊥BC于G,则四边形AFGD是矩形,
∵在Rt△AFB中,∠B=60°,AB=6,
∴∠BAF=30°,
∴BF=$\frac{1}{2}$×6=3,
∴AF=$\sqrt{A{B}^{2}-B{F}^{2}}$=3$\sqrt{3}$,
∴DG=3$\sqrt{3}$,
∵AD=2,
∴FG=2,
∴CG=BC-BF-FG=1,
∴在Rt△CGD中,CD=$\sqrt{C{G}^{2}+D{G}^{2}}$=2$\sqrt{7}$.
故答案为:2$\sqrt{7}$.
点评 考查了勾股定理,含30度角的直角三角形,矩形的判定与性质,解题的关键是添加辅助线构造直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列变形中,正确的是( )
| A. | 由5x=-4得x=-$\frac{5}{4}$ | B. | 由4x+2=3x-1得4x+3x=2-1 | ||
| C. | 由$\frac{x}{5}$-1=2得x-5=2 | D. | 由4x-3=2x-2得2x=1 |
8. 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排序,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…根据这个规律,则第2018个点的横坐标为( )
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排序,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…根据这个规律,则第2018个点的横坐标为( )
 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排序,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…根据这个规律,则第2018个点的横坐标为( )
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排序,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…根据这个规律,则第2018个点的横坐标为( )| A. | 44 | B. | 45 | C. | 46 | D. | 47 |
15.下列各式中不能用平方差公式计算的是( )
| A. | (2x+y)(2x-y) | B. | (x-y)(y-x) | C. | (-x+y)(-x-y) | D. | (x+y)(-x+y) |
12.下列变形,属于因式分解的有( )
①x2-16=(x+4)(x-4)②x2+3x-16=x(x+3)-16
③(x+4)(x-4)=x2-16 ④x2+x=x(x+1)
①x2-16=(x+4)(x-4)②x2+3x-16=x(x+3)-16
③(x+4)(x-4)=x2-16 ④x2+x=x(x+1)
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13. 如图,将?ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B为( )
如图,将?ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B为( )
 如图,将?ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B为( )
如图,将?ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B为( )| A. | 124° | B. | 114° | C. | 104° | D. | 66° |
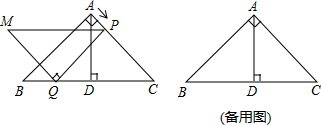
 如图,点B、E、C、F在一条直线上,∠B=∠DEF,AB=DE,BE=CF,∠F=68°,求∠ACB的度数.
如图,点B、E、C、F在一条直线上,∠B=∠DEF,AB=DE,BE=CF,∠F=68°,求∠ACB的度数.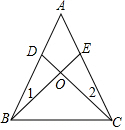 如图,在△ABC中,D,E分别是AB,AC边上的点,且∠1=∠2,CD=BE.CD与BE相交于点O.求证:
如图,在△ABC中,D,E分别是AB,AC边上的点,且∠1=∠2,CD=BE.CD与BE相交于点O.求证: