题目内容
17．一个长方形的长与宽的比为5：3，对角线长为$\sqrt{6800}$，求这个长方形的长和宽．分析 可设长方形的长是5x，宽是3x，由于对角线长为$\sqrt{6800}$，根据勾股定理可得方程（5x）2+（3x）2=（$\sqrt{6800}$）2，解方程即可求解．
解答 解：设长方形的长是5x，宽是3x，则
（5x）2+（3x）2=（$\sqrt{6800}$）2，
解得x=±10$\sqrt{2}$（负值舍去），
5x=50$\sqrt{2}$，
3x=30$\sqrt{2}$．
故这个长方形的长是50$\sqrt{2}$，宽是30$\sqrt{2}$．
点评 本题考查了勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．由对角线长为$\sqrt{6800}$，根据勾股定理得到方程是解题的关键．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
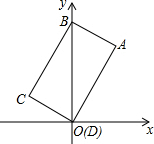如图，把矩形ABCD按如图所示方式放置，若点A的坐标为（2，3），点B的坐标为（0，4）．