题目内容
1.在Rt△ABC中,∠C=90°,BC=8,AB=10,若点G是△ABC的重心,则cos∠GCB=$\frac{4}{5}$.分析 根据直角三角形的性质,可得CD的长,根据三角形中位线的性质,可得CE的长,根据锐角三角函数的定义,可得答案.
解答 解:如图: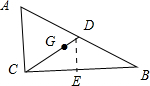
作DE⊥BC于E,
由点G是△ABC的重心,得
G在中线CD上,
CD=$\frac{1}{2}$AB=$\frac{1}{2}$×10=5.
由DE⊥BC,AC⊥BC,CD是中线,得
CE=$\frac{1}{2}$BC=$\frac{1}{2}$×8=4,
cos∠GCB=$\frac{CE}{CD}$=$\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 本题考查了三角形的重心,利用直角三角形的性质得出CD的长是解题关键,又利用了三角形中位线的性质,锐角三角函数.

练习册系列答案
相关题目
12.下面说法中错误的是( )
| A. | 10000万精确到万位 | B. | 2.580精确到千分位 | ||
| C. | 0.0250有3个有效数字 | D. | 17049保留3个有效数字为1.71×104 |
9.已知二次函数y=x2+bx-9图象上A、B两点关于原点对称,若经过A点的反比例函数的解析式是y=$\frac{8}{x}$,则该二次函数的对称轴是直线( )
| A. | x=1 | B. | x=$\frac{4}{9}$ | C. | x=-1 | D. | x=-$\frac{4}{9}$ |