题目内容
9.已知二次函数y=x2+bx-9图象上A、B两点关于原点对称,若经过A点的反比例函数的解析式是y=$\frac{8}{x}$,则该二次函数的对称轴是直线( )| A. | x=1 | B. | x=$\frac{4}{9}$ | C. | x=-1 | D. | x=-$\frac{4}{9}$ |
分析 设A点坐标为(a,$\frac{8}{a}$),则可求得B点坐标,把两点坐标代入抛物线的解析式可得到关于a和b的方程组,可求得b的值,则可求得二次函数的对称轴.
解答 解:∵A在反比例函数图象上,
∴可设A点坐标为(a,$\frac{8}{a}$),
∵A、B两点关于原点对称,
∴B点坐标为(-a,-$\frac{8}{a}$),
又∵A、B两点在二次函数图象上,
∴代入二次函数解析式可得$\left\{\begin{array}{l}{{a}^{2}+ab-9=\frac{8}{a}}\\{{a}^{2}-ab-9=-\frac{8}{a}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=3\sqrt{2}}\\{b=\frac{4}{9}}\end{array}\right.$或$\left\{\begin{array}{l}{a=-3\sqrt{2}}\\{b=\frac{4}{9}}\end{array}\right.$,
∴二次函数对称轴为x=-$\frac{4}{9}$.
故选:D.
点评 本题主要考查二次函数的性质,待定系数法求二次函数解析式,根据条件先求得b的值是解题的关键,注意掌握关于原点对称的两点的坐标的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20. 如图,下面说法中错误的是( )
如图,下面说法中错误的是( )
 如图,下面说法中错误的是( )
如图,下面说法中错误的是( )| A. | 点B在直线MC上 | B. | 点A在直线BC外 | C. | 点C在线段MB上 | D. | 点M在线段BC上 |
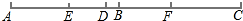 如图,已知线段AB和CD的公共部分BD=$\frac{1}{4}$AB=$\frac{1}{5}$CD,线段AB、CD的整点E、F之间距离是20cm,求BD的长.
如图,已知线段AB和CD的公共部分BD=$\frac{1}{4}$AB=$\frac{1}{5}$CD,线段AB、CD的整点E、F之间距离是20cm,求BD的长.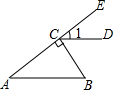 如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于35度.
如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于35度.