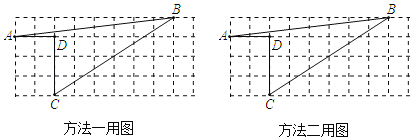Question

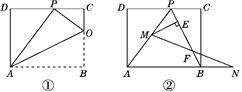
【题目】如图1、2，已知四边形ABCD为正方形，在射线AC上有一动点P，作PE⊥AD（或延长线）于E，作PF⊥DC（或延长线）于F，作射线BP交EF于G．

（1）在图1中，设正方形ABCD的边长为2，四边形ABFE的面积为y，AP=x，求y关于x的函数表达式；

（2）结论：GB⊥EF对图1，图2都是成立的，请任选一图形给出证明；

（3）请根据图2证明：△FGC∽△PFB．

Answer 1

【答案】（1）y=x2+2；(2)证明见解析；（3）证明见解析.

【解析】

试题分析：（1）根据题意得出S四边形ABFE=4﹣ED×DF﹣BC×FC进而得出答案；

（2）首先利用正方形的性质进而证明△FPE≌△BHP（SAS），即可得出△FPG∽△BPH，求出即可；

（3）首先得出△DPC≌△BPC（SAS），进而利用相似三角形的判定得出△FGC∽△PFB．

试题解析：（1）解：∵PE⊥AD，PF⊥DC，

∴四边形EPFD是矩形，

∵AP=x，

∴AE=EP=DF=x，

DE=PF=FC=2﹣x，

∴S四边形ABFE=4﹣EDDF﹣BCFC=x2+2；

（2）证明：如图1，延长FP交AB于H，

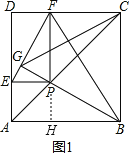
∵PF⊥DC，PE⊥AD，

∴PF⊥PE，PH⊥HB，

即∠BHP=90°，

∵四边形ABCD是正方形，

∴AC平分∠DAB，

∴可得PF=FC=HB，EP=PH，

在△FPE与△BHP中

，

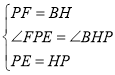∴△FPE≌△BHP（SAS），

∴∠PFE=∠PBH，

又∵∠FPG=∠BPH，

∴△FPG∽△BPH，

∴∠FGP=∠BHP=90°，

即GB⊥EF；

（3）证明：如图2，连接PD，

∵GB⊥EF，

∴∠BPF=∠CFG①，

在△DPC和△BPC中

，

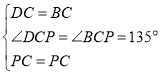∴△DPC≌△BPC（SAS），

∴PD=PB，

而PD=EF，∴EF=PB，

又∵GB⊥EF，

∴PF2=FGEF，

∴PF2=FGPB，

而PF=FC，

∴PFFC=FGPB，

∴②，

∴由①②得△FGC∽△PFB．