ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌгаРэЪ§ aЃЌbЃЌc ЗжБ№ЖдгІЪ§жсЩЯЕФЕу A,B,C,Шєa 2![]() |b 4| 0 ЃЌЙигк xЁЂy ЕФЕЅЯюЪН3(c 3)x
|b 4| 0 ЃЌЙигк xЁЂy ЕФЕЅЯюЪН3(c 3)x![]() y
y![]() гы y
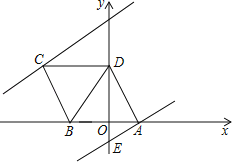
гы y![]() x ЪЧЭЌРрЯю. ЮвУЧАбЪ§жсЩЯСНЕужЎМфЕФОрРыгУБэЪОСНЕуЕФДѓаДзжФИвЛЦ№БъМЧЃЌР§ШчЃЌЕу A гыЕу B МфЕФОрРыМЧзї AB.
x ЪЧЭЌРрЯю. ЮвУЧАбЪ§жсЩЯСНЕужЎМфЕФОрРыгУБэЪОСНЕуЕФДѓаДзжФИвЛЦ№БъМЧЃЌР§ШчЃЌЕу A гыЕу B МфЕФОрРыМЧзї AB.
![]()
![]()
(1)Чѓ aЃЌbЃЌc ЕФжЕЃЛ
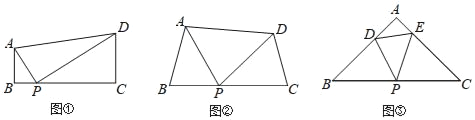
(2)Еу P Дг C ЕуГіЗЂвдУПУы 1 ИіЕЅЮЛГЄЖШдкЪ§жсЩЯАДвдЯТЙцТЩЭљЗЕдЫЖЏЃКЕквЛЛиКЯЃЌДгЕу C ЕНЕу B ЕНЕу A ЛиЕНЕу CЃЛЕкЖўЛиКЯЃЌДгЕу C ЕН BC ЕФжаЕу D ЕН CA ЕФжаЕу D1 ЛиЕНЕу CЃЛЕкШ§ЛиКЯЃЌДгЕу C ЕН CD ЕФжаЕу D2 ЕН CD1 ЕФжаЕу D3 ЛиЕНЕу CЁЁЃЌШчДЫбЛЗЯТШЅЃЌШєЕк t УыЪБТњзу PB+2PC=AC+1ЃЌЧѓ t ЕФзюДѓжЕЃЛ
(3)дкЃЈ2ЃЉЕФЬѕМўЯТЃЌP ЕуЕквЛДЮДг C ЕуГіЗЂЕФЭЌЪБЃЌЪ§жсЩЯЕФЖЏЕу MЁЂN ЗжБ№Дг A ЕуКЭ B ЕуЯђгвдЫЖЏЃЌЫйЖШЗжБ№ЮЊУПУы 1 ИіЕЅЮЛГЄЖШКЭУПУы 2 ИіЕЅЮЛГЄЖШЃЌP ЕуЭъГЩЕквЛИіЛиКЯКѓЭЃжЙдк C ЕуЃЌЕБ MP=2MN ЪБЃЌ t ЕФжЕЪЧ ЃЈжБНгЬюД№АИЃЉ
ЁОД№АИЁПЃЈ1ЃЉa=2ЃЌb=Ѓ4ЃЌc=Ѓ1ЃЛЃЈ2ЃЉзюДѓжЕЮЊ![]() УыЃЛЃЈ3ЃЉ
УыЃЛЃЈ3ЃЉ![]() Уы.
Уы.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнОјЖджЕКЭХМДЮУнЕФЗЧИКадПЩвдЧѓГіaЁЂbЃЌдйИљОнЭЌРрЯюЕФЖЈвхЧѓcМДПЩ.
ЃЈ2ЃЉЪзЯШИљОнЕквЛЛиКЯМЦЫуГіТњзуPB+2PC=AC+1ЪБЕФtжЕЃЌДгЖјЕУЕНвЊТњзуPB+2PC=AC+1ЕФЕуPЫљЖдгІЕФЪ§ЃЌНјЖјЗжЮіЕкМИЛиКЯЕНДяВЛСЫетИіЪ§ЃЌДгЖјЧѓзюДѓжЕЃЛ
ЃЈ3ЃЉЗжЮіNзЗЩЯMЪБtЕФжЕЃЌОнДЫНјааЗжРрЬжТл.
ЃЈ1ЃЉЁп![]() ЃЌ3(c 3)x
ЃЌ3(c 3)x![]() y
y![]() гы y
гы y![]() x ЪЧЭЌРрЯю
x ЪЧЭЌРрЯю
ЁрaЃ2=0ЃЌb+4=0ЃЌ|c+2|=1Чвc+3Ёй0ЃЌ
Ёрa=2ЃЌb=Ѓ4ЃЌc=Ѓ1.
ЃЈ2ЃЉгЩЃЈ1ЃЉжЊЃЌЕуAЖдгІЕФЪ§ЮЊ2ЃЌЕуBЖдгІЕФЪ§ЮЊЃ4ЃЌЕуCЖдгІЕФЪ§ЮЊЃ1ЃЌдђAC=3ЃЌ
ЕквЛЛиКЯЃКЕБЕуPДгCЕНBЪБЃЌCP=tЃЌBP=3ЃtЃЌ
ЁпPB+2PC=AC+1
Ёр3Ѓt+2t=4ЃЌдђt=1ЃЌДЫЪБЕуPЖдгІЕФЪ§ЮЊЃ2ЃЌ
ЕБЕуPДгCЕНAЪБЃЌCP=tЃ6ЃЌBP=3+tЃ6=tЃ3ЃЌ
ЁпPB+2PC=AC+1
ЁрtЃ3+2(tЃ6)=4ЃЌдђt=![]() ЃЌДЫЪБЕуPЖдгІЕФЪ§ЮЊ
ЃЌДЫЪБЕуPЖдгІЕФЪ§ЮЊ![]() ЃЌ
ЃЌ
ЭЈЙ§МЦЫуПЩЕУЃЌD4ЖдгІЕФЪ§ЮЊ![]() ЃЌD5ЖдгІЕФЪ§ЮЊ
ЃЌD5ЖдгІЕФЪ§ЮЊ![]() ЃЌD6ЖдгІЕФЪ§ЮЊ
ЃЌD6ЖдгІЕФЪ§ЮЊ![]() >Ѓ2ЃЌD7ЖдгІЕФЪ§ЮЊ
>Ѓ2ЃЌD7ЖдгІЕФЪ§ЮЊ![]() <
<![]() ЃЌЫљвдtЕФзюДѓжЕдкЕкШ§ЛиКЯЕуPДгD5ЛиЕНЕуCЪБШЁЕУ.
ЃЌЫљвдtЕФзюДѓжЕдкЕкШ§ЛиКЯЕуPДгD5ЛиЕНЕуCЪБШЁЕУ.
ДЫЪБCP= ![]() ЃЌBP=
ЃЌBP= ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
ЙЪТњзуPB+2PC=AC+1ЪБЃЌtЕФзюДѓжЕЮЊ![]() Уы.
Уы.
ЃЈ3ЃЉгЩЬтПЩЕУЃЌAC==BC=3ЃЌЕуPдЫЖЏТЗГЬЮЊtЃЌЕуMдЫЖЏТЗГЬЮЊtЃЌЕуNдЫЖЏТЗГЬЮЊ2tЃЌ
Сю2tЃt=6ЃЌНтЕУt=6ЃЌдђдЫЖЏ6УыКѓNзЗЩЯMЃЌ
ЂйзЗЩЯЧАЃЈ![]() ЃЉЃКMN=6+tЃ2t=6ЃtЃЌ
ЃЉЃКMN=6+tЃ2t=6ЃtЃЌ
ЕБ![]() ЪБЃЌMP=t+3+t=2t+3ЃЌдђ2t+3=2(6Ѓt)ЃЌНтЕУ
ЪБЃЌMP=t+3+t=2t+3ЃЌдђ2t+3=2(6Ѓt)ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌMP= t+3+(6Ѓt)=9ЃЌдђ9=2(6Ѓt)ЃЌНтЕУ
ЪБЃЌMP= t+3+(6Ѓt)=9ЃЌдђ9=2(6Ѓt)ЃЌНтЕУ![]() ЃЌВЛТњзуЬѕМўЩсШЅЃЛ
ЃЌВЛТњзуЬѕМўЩсШЅЃЛ
ЂкзЗЩЯКѓЃЈ![]() ЃЉЃКMN=2tЃ6Ѓt =tЃ6ЃЌ
ЃЉЃКMN=2tЃ6Ѓt =tЃ6ЃЌ
ЕБ![]() ЪБЃЌMP=9Ѓt+t=9ЃЌдђ9=2(tЃ6)ЃЌНтЕУ
ЪБЃЌMP=9Ѓt+t=9ЃЌдђ9=2(tЃ6)ЃЌНтЕУ![]() ЃЌВЛТњзуЬѕМўЩсШЅЃЌ
ЃЌВЛТњзуЬѕМўЩсШЅЃЌ
ЕБ![]() ЪБЃЌMP= tЃ9+t=2tЃ9ЃЌдђ2tЃ9=2(tЃ6)ЃЌЮоНтЃЛ
ЪБЃЌMP= tЃ9+t=2tЃ9ЃЌдђ2tЃ9=2(tЃ6)ЃЌЮоНтЃЛ
злЩЯЫљЪіЃЌtжЕЮЊ![]() Уы.
Уы.

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИЁОЬтФПЁПЙЋдАЕФУХЦБМлИёЙцЖЈШчЯТБэЃК
ЙКЦБеХЪ§ | 1 ЕН 50 еХ | 51 ЕН 100 еХ | 101 ЕН 150еХ | 150 еХвдЩЯ |
УПеХЦБЕФМлИё | 12 дЊ | 10 дЊ | 8 дЊ | ГЌЙ§ 150 еХЕФВПЗж 7 дЊ |
ФГаЃЦпФъМЖЃЈ1ЃЉЃЈ2ЃЉСНИіАрЙВ 104 ШЫЃЌЦфжаЃЈ1ЃЉАр 40 ЖрШЫЃЌВЛзу 50 ШЫЃЌОЙРЫуЃЌШчЙћСНИіАрЖМвдАрЮЊЕЅЮЛЙКЦБЃЌдђвЛЙВгІИЖ 1136 дЊЃЌЮЪЃК
(1)ШєСНАрСЊКЯЦ№РДзїЮЊвЛИіЭХЬхЙКЦБЃЌПЩЪЁЖрЩйЧЎЃП
(2)СНАрбЇЩњИїгаЖрЩйШЫЃП
(3)ШєЦпФъМЖЃЈ3ЃЉАрга n ШЫЃЈ46<n<55ЃЉгыЃЈ1ЃЉ,ЃЈ2ЃЉАрвЛЦ№ШЅгЮдАЃЌФГЩЬМвдожњЃЌжЇИЖШ§ИіАрЕФЫљгаУХЦБЗбЃЌдђИУЩЬМвзюЩйЛЈЗб дЊЃЈгУКЌ n ЕФЪНзгБэЪОЃЉ