Question

【题目】如图，一次函数的图像分别交y轴、x轴交于点A、B，点P从点B出发，沿射线BA以每秒1个单位的速度出发，设点P的运动时间为t秒.

（1）点P在运动过程中，若某一时刻，△OPA的面积为6,求此时P的坐标；

（2）在整个运动过程中，当t为何值时，△AOP为等腰三角形？（只需写出t的值，无需解答过程）

Answer 1

【答案】（1）（2,4.5），（-2，7.5）；（2）2.8,4,5,16

【解析】试题分析：（1）先求出△OPA的面积为6时BP的长，再求出点P的坐标；（2）分别讨论AO=AP，AP=OP和AO=OP三种情况.

解：（1）在y=-x+6中，令x=0，得y=6，令y=0，得x=8，

∴A（0，6），B（8，0），

∴OA=6，OB=8，∴AB=10，

∴AB边上的高为6×8÷10=，

∵P点的运动时间为t，∴BP=t，则AP=，

当△AOP面积为6时，则有AP×=6，即×=6，解得t=7.5或12.5，

过P作PE⊥x轴，PF⊥y轴，垂足分别为E、F，

则PE==4.5或7.5，BE==6或10，

则点P坐标为（8-6,4.5）或（8-10,7.5），即（2,4.5）或（-2,7.5）；

（2）由题意可知BP=t，AP=，

当△AOP为等腰三角形时，有AP=AO、AP=OP和AO=OP三种情况．
①当AP=AO时，则有=6，解得t=4或16；

②当AP=OP时，过P作PM⊥AO，垂足为M，如图1，

则M为AO中点，故P为AB中点，此时t=5；

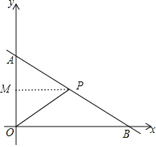
图1 图2

③当AO=OP时，过O作ON⊥AB，垂足为N，过P作PH⊥OB，垂足为H，如图2，

则AN=AP=（10-t），
∵PH∥AO，∴△AOB∽△PHB，

∴=，即=,∴PH=t，

又∠OAN+∠AON=∠OAN+PBH=90°，

∴∠AON=∠PBH，又∠ANO=∠PHB，
∴△ANO∽△PHB，
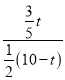=，即=，解得t=；

综上可知当t的值为、4、5和16时，△AOP为等腰三角形．